
【题目】若四边形的两条对角线相等,则顺次连接该四边形各边中点所得的四边形是( )
A.梯形
B.矩形
C.菱形
D.正方形
【答案】C
【解析】解:如图,AC=BD,E、F、G、H分别是线段AB、BC、CD、AD的中点, ∴EH、FG分别是△ABD、△BCD的中位线,EF、HG分别是△ACD、△ABC的中位线,∴EH=FG= ![]() BD,EF=HG=
BD,EF=HG= ![]() AC,
AC,
∵AC=BD
∴EH=FG=FG=EF,
则四边形EFGH是菱形.故选C.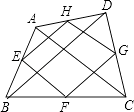
【考点精析】掌握三角形中位线定理和菱形的判定方法是解答本题的根本,需要知道连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.


科目:初中数学 来源: 题型:
【题目】第六次人口普查显示,湛江市常住人口数约为6990000人,数据6990000用科学记数法表示为( )
A. 69.9×105B. 0.699×107
C. 6.99×106D. 6.99×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题.
例:若代数式![]() 的值是常数2,则a的取值范围 2≤a≤4 .
的值是常数2,则a的取值范围 2≤a≤4 .
分析:原式=|a﹣2|+|a﹣4|,而|a|表示数x在数轴上的点到原点的距离,|a﹣2|表示数a在数轴上的点到数2的点的距离,所以我们可以借助数轴进行分析.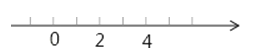
解:原式=|a﹣2|+|a﹣4|
在数轴上看,讨论a在数2表示的点左边;在数2表示的点和数4表示的点之间还是在数4表示的点右边,分析可得a的范围应是2≤a≤4.
(1)此例题的解答过程了用了哪些数学思想?请列举.
(2)化简![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表给出了某班6名同学的身高情况(单位:cm).
学生 | A | B | C | D | E | F | |
身高(单位:cm) | 165 | ____ | 166 | ____ | ____ | 172 | |
身高与班级平 | 均身高的差值) | -1 | +2 | ____ | -3 | +4 | ____ |
(1)完成表中空的部分;
(2)他们6人中最高身高比最矮身高高多少?
(3)如果身高达到或超过平均身高时叫达标身高,那么这6名同学身高的达标率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com