B
分析:先根据△ABC中,∠BAC=90°,AB=AC求出∠B、∠DAE的度数,再根据AD=AE可得出∠AED的度数,由三角形内角和定理求出∠ADC的度数,进而可得出结论.
解答:∵△ABC中,∠BAC=90°,AB=AC,
∴∠B=∠C=

=45°,
∵△ABD中,∠B=45°,∠BAD=30°,
∴∠ADC=∠B+∠BAD=45°+30°=75°,
∵∠BAC=90°,∠BAD=30°,
∴∠DAC=90°-30°=60°,
∵AD=AE,
∴∠DAE=∠DEA=60°,
∴∠ADE=180°-∠DAE-∠DEA=180°-60°-60°=60°,
∴∠EDC=∠ADC-∠ADE=75°-60°=15°.
故选B.
点评:本题考查的是等腰三角形的性质,解答此类题目时要注意三角形内角和定理、三角形外角的性质等知识的具体运用.

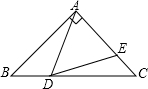 如图所示,已知△ABC中,∠BAC=90°,AB=AC,∠BAD=30°,AD=AE,则∠EDC的度数为
如图所示,已知△ABC中,∠BAC=90°,AB=AC,∠BAD=30°,AD=AE,则∠EDC的度数为 =45°,
=45°,
