
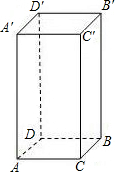
 如图,已知长方体的长2cm、宽为1cm、高为4cm.一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是5cm.
如图,已知长方体的长2cm、宽为1cm、高为4cm.一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是5cm. 分析 要求长方体中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.
解答 解:如图:
根据题意,如上图所示,最短路径有以下三种情况:
(1)沿AA′,A′C′,C′B′,B′B剪开,得图(1)AB′2=AB2+BB′2=(2+1)2+42=25;
(2)沿AC,CC′,C′B′,B′D′,D′A′,A′A剪开,得图(2)AB′2=AC2+B′C2=22+(4+1)2=4+25=29;
(3)沿AD,DD′,B′D′,C′B′,C′A′,AA′剪开,得图(3)AB′2=AD2+B′D2=12+(4+2)2=1+36=37;
综上所述,最短路径应为(1)所示,所以AB′2=25,即AB′=5cm.
故答案为5cm.
点评 本题考查了平面展开最短路径问题,将长方体从不同角度展开,是解决此类问题的关键,注意不要漏解.


科目:初中数学 来源: 题型:选择题
| A. | 129 | B. | 120 | C. | 108 | D. | 96 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
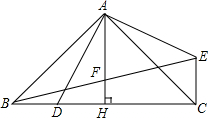 已知:AC=AB,AD=AE,AD⊥AE,AB⊥AC,垂足均为点A,连接BE,AH⊥BC,垂足为点H,AH与BE相交于F.求证:BF=EF.
已知:AC=AB,AD=AE,AD⊥AE,AB⊥AC,垂足均为点A,连接BE,AH⊥BC,垂足为点H,AH与BE相交于F.求证:BF=EF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.12×109 | B. | 1.2×107 | C. | 1.2×108 | D. | 12×107 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com