
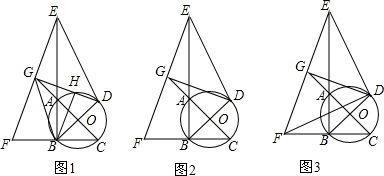
���� ��1������AC��BD��OB=OD�õ���GOD=90�㣬GD=GB���Ӷ��õ���BGD=2��DGO��Ȼ����á�DGO=��HBD���ɵõ�BGD=2��HBD��
��2������G��GG1��BC������ΪG1������G��GG2��DC������ΪG2���õ��ı���GG1BPΪ���Σ��ı���GG1CG2�������Ρ��ı���PADG2Ϊ�����Σ��Ӷ�֤�á�FGG1�ա�DGG2������ȫ�������ε����ʵõ�GE=GD���ɵõ���DGE�ǵ���ֱ�������Σ�
��3���ɣ�1����֪�ı���ABCD�����������FD=2$\sqrt{10}$���ɣ�2��֪DG��EF�Ĵ�ֱƽ���ߵõ�DI=$\frac{2}{3}$$\sqrt{10}$��Ȼ�����IE2=DE2+ID2=��2$\sqrt{10}$��2+��$\frac{2}{3}$$\sqrt{10}$��2=$\frac{400}{9}$���EI=$\frac{20}{3}$��
��� ��1��֤������AC��BD��OB=OD��
���GOD=90�㣬GD=GB��
���BGO=��DGO��
���BGD=2��DGO��
��BD�ǡ�O��ֱ����
���BHD=90�㣬
���DGO+��ODG=90�㣬��HBD+��ODG=90�㣬
���DGO=��HBD��
���BGD=2��HBD��
��2������G��GG1��BC������ΪG1������G��GG2��DC������ΪG2����GG1=GG2��
��AC��BD�ǡ�O���������ഹֱ��ֱ����
���ı���ABCD�������Σ�
���BCD=��ABC=��ADC=90�㣬GG1��CF��CA�ǡ�BCD��ƽ���ߣ�
���AGPΪ����ֱ�������Σ���PBF=��ADG2=90�㣬
��AP=GP���ı���GG1BPΪ���Σ��ı���GG1CG2�������Σ�
��GP=G1B��
ͬ�����ı���PADG2Ϊ�����Σ�AP=DG2��
�ߡ�GG1F=90�㣬��ABF=90�㣬
��GG1��BE��
���FGG1=��GEP��
���G2GD=��FGG1
���֤��FGG1�ա�DGG2��
��FG1=DG2��
��FG1=BG1��
��$\frac{FG}{GE}=\frac{F{G}_{1}}{{G}_{1}B}$=1��
��FG=GE��
��GE=GD��
���DGE�ǵ���ֱ�������Σ�
��3���ɣ�1����֪�ı���ABCD�������Σ�
��AC=2OC=2$\sqrt{2}$��
��AD2+DC2=AC2��
��AD=DC=$\frac{\sqrt{2}}{2}$��2$\sqrt{2}$=2��
��tan��DFC=$\frac{DC}{FC}$=$\frac{1}{3}$��
��FC=6��
��FD2=DC2+CF2��
��FD=2$\sqrt{10}$��
�ɣ�2��֪DG��EF�Ĵ�ֱƽ���ߣ�
��DF=DE=2$\sqrt{5}$��
���DFC=��FED=45�㣬
���FDE=180��-45��-45��=90�㣬
���IED+��EID=90�㣬
�֡ߡ�BFI+��BIF=90�㣬
��tan��IED=tan��DFC=$\frac{1}{3}$=$\frac{DI}{ED}$��
��DI=$\frac{2}{3}$$\sqrt{10}$��
��IE2=DE2+ID2=��2$\sqrt{10}$��2+��$\frac{2}{3}$$\sqrt{10}$��2=$\frac{400}{9}$��
��EI=$\frac{20}{3}$��
���� ���⿼����ȫ�������ε��ж������ʡ�ƽ���ߵ��ж������ʡ����������ε��ж��Լ����Ǻ�����������һ���Ѷȣ��ر��ǣ�2���У���Ҫͨ����������֤�������κ��������Ǻ���������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
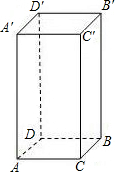 ��ͼ����֪������ij�2cm����Ϊ1cm����Ϊ4cm��һֻ��������س�����ı����A������B��㣬��ô������·�������̵�·����5cm��
��ͼ����֪������ij�2cm����Ϊ1cm����Ϊ4cm��һֻ��������س�����ı����A������B��㣬��ô������·�������̵�·����5cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
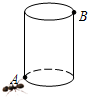 ��ͼ����һ���ױ߰뾶Ϊ6cm����Ϊ24cm��Բ������Բ���µ���ĵ�A����һֻ���ϣ�����Ե��ϵ�������A����Ե�B����ʳ����ʣ�����Ҫ���е����·��Խ�Ƕ��٣�
��ͼ����һ���ױ߰뾶Ϊ6cm����Ϊ24cm��Բ������Բ���µ���ĵ�A����һֻ���ϣ�����Ե��ϵ�������A����Ե�B����ʳ����ʣ�����Ҫ���е����·��Խ�Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
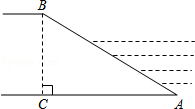 ��ͼ���ӵ̺����ӭˮ��AB���±���1��$\sqrt{3}$���̸�BC=10m��������AB�ij���
��ͼ���ӵ̺����ӭˮ��AB���±���1��$\sqrt{3}$���̸�BC=10m��������AB�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
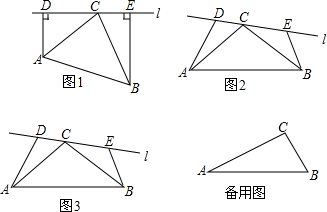
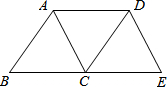 ��ͼ������ABC��BC����ƽ�Ƶõ���DCE������AD�������������ܹ��ж��ı���ACEDΪ���ε��ǣ�������
��ͼ������ABC��BC����ƽ�Ƶõ���DCE������AD�������������ܹ��ж��ı���ACEDΪ���ε��ǣ�������| A�� | ��ACB=60�� | B�� | ��B=60�� | C�� | AB=BC | D�� | AC=BC |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com