
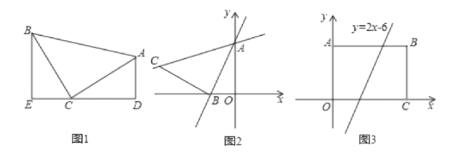
【题目】(1)模型建立,如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.求证:△BEC≌△CDA;
(2)模型应用:
①已知直线y=![]() x+3与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线.求直线AC的解析式;
x+3与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线.求直线AC的解析式;
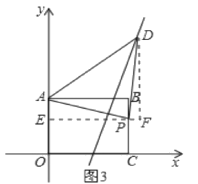
②如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A,C分别在坐标轴上,P是线段BC上动点,已知点D在第一象限,且是直线y=2x-6上的一点,若△APD是不以A为直角顶点的等腰直角三角形,请直接写出所有符合条件的点D的坐标.
【答案】(1)见解析(2)y=![]() x+4(3)(4,2)或(
x+4(3)(4,2)或(![]() )或(
)或(![]() ).
).
【解析】
(1)由条件可求得∠EBC=∠ACD,利用AAS可证明△BEC≌△CDA;
(2)由直线解析式可求得A、B的坐标,利用模型结论可得CE=BO,BE=AO,从而可求得C点坐标,利用待定系数法可求得直线AC的解析式;
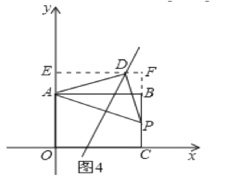
(3)分三种情况考虑:如图2所示,当∠ADP=90°时,AD=PD,设D点坐标为(x,2x-6),利用三角形全等得到x+6-(2x-6)=8,得x=4,易得D点坐标;如图3所示,当∠APD=90°时,AP=PD,设点P的坐标为(8,m),表示出D点坐标为(14-m,m+8),列出关于m的方程,求出m的值,即可确定出D点坐标;如图4所示,当∠ADP=90°时,AD=PD时,同理求出D的坐标.
(1)∵∠ACB=90,
∴∠EBC+∠BCE=∠BCE+∠ACD=90,
∴∠EBC=∠ACD,
在△BEC和△CDA中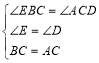 ,
,
∴△BEC≌△CDA(AAS);
(2)如图1,
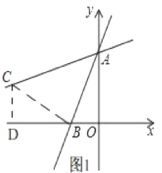
过点B作BC⊥AB交直线l![]() 于C过C作CD⊥x轴于点D,
于C过C作CD⊥x轴于点D,
在y=![]() x+4中,令y=0可求得x=3,令x=0可求得y=4,
x+4中,令y=0可求得x=3,令x=0可求得y=4,
∴OA=4,OB=3,
同(1)可证得△CDB≌△BAO,
∴CD=BO=3,BD=AO=4,
∴OD=4+3=7,
∴C(7,3),且A(0,4),
设直线AC解析式为y=kx+4,把C点坐标代入可得7k+4=3,解得k=![]() ,
,
∴直线AC解析式为y=![]() x+4;
x+4;
(3)如图2,
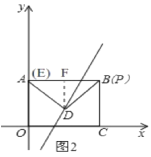
当∠ADP=90时,AD=PD,
过点P作PE⊥OA于E,过点D作DF⊥PE于F,
∴点E与点A重合,∴DF=![]() AB=4
AB=4
设D点坐标为(x,2x6),6(2x6)=4,得x=4,
易得D点坐标(4,2);
如图3,当∠APD=90°时,AP=PD,
过点P作PE⊥OA于E,过点D作DF⊥PE于F,
设点P的坐标为(8,m),易证,△APE≌△PDF,
∴PF=AE=6m,DF=PE=8,
∴D点坐标为(1m,m+8),
∴m+8=2(14m)6,得m=![]() ,
,
∴D点坐标(![]() );
);
如图4,当∠ADP=90°时,AD=PD时,同理得D点坐标(![]() ),
),
综上可知满足条件的点D的坐标分别为(4,2)或(![]() )或(
)或(![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
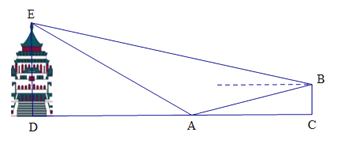
【题目】气魄雄伟的大礼堂座落在渝中区学田湾,它是一座仿古民族建筑.“五一”期间,小明和妈妈到重庆大礼堂参观游玩.参观结束后,穿过人民广场到达A处,回望礼堂,更显气势雄伟,金碧辉煌.此时,在A点观察到礼堂顶端的仰角为30°,沿着坡度为1:3的斜坡AB走一段距离到达B点,观察到礼堂顶端 的仰角是22°,测得点A与BC之间的水平距离![]() 米,则大礼堂的高度DE为( )米.(精确到1米.参考数据:
米,则大礼堂的高度DE为( )米.(精确到1米.参考数据: ![]() ,
, ![]() .)
.)
A. 58 B. 60 C. 62 D. 64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们给出如下定义:数轴上给定两点![]() ,
,![]() 以及一条线段
以及一条线段![]() ,若线段
,若线段![]() 的中点
的中点![]() 在线段
在线段![]() 上(点
上(点![]() 可以与点
可以与点![]() 或
或![]() 重合),则称点
重合),则称点![]() 与点
与点![]() 关于线段
关于线段![]() 径向对称.下图为点
径向对称.下图为点![]() 与点
与点![]() 关于线段
关于线段![]() 径向对称的示意图.
径向对称的示意图.

解答下列问题:
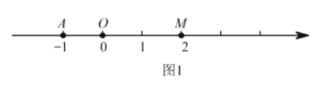
如图1,在数轴上,点![]() 为原点,点
为原点,点![]() 表示的数为-1,点
表示的数为-1,点![]() 表示的数为2.
表示的数为2.
(1)①点![]() ,
,![]() ,
,![]() 分别表示的数为-3,
分别表示的数为-3,![]() ,3,在
,3,在![]() ,
,![]() ,
,![]() 三点中, 与点
三点中, 与点![]() 关于线段
关于线段![]() 径向对称;
径向对称;
②点![]() 表示的数为
表示的数为![]() ,若点
,若点![]() 与点
与点![]() 关于线段
关于线段![]() 径向对称,则
径向对称,则![]() 的取值范围是 ;
的取值范围是 ;
(2)在数轴上,点![]() ,
,![]() ,
,![]() 表示的数分别是-5,-4,-3,当点
表示的数分别是-5,-4,-3,当点![]() 以每秒1个单位长度的速度向正半轴方向移动时,线段
以每秒1个单位长度的速度向正半轴方向移动时,线段![]() 同时以每秒3个单位长度的速度向正半轴方向移动.设移动的时间为
同时以每秒3个单位长度的速度向正半轴方向移动.设移动的时间为![]() (
(![]() )秒,问
)秒,问![]() 为何值时,线段
为何值时,线段![]() 上至少存在一点与点
上至少存在一点与点![]() 关于线段
关于线段![]() 径向对称.
径向对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列每对数在数轴上的对应点间的距离,3与5,4与﹣2, ﹣4与3, ﹣1与﹣5.并回答下列各题:
![]()
(1)数轴上表示4和﹣2两点间的距离是 ;表示﹣1和﹣5两点间的距离是 .
(2)若数轴上的点A表示的数为x,点B表示的数为﹣3.
①数轴上A、B两点间的距离可以表示为 (用含x的代数式表示);
②如果数轴上A、B两点间的距离为|AB|=1,求x的值.
(3)直接写出代数式![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1) ∠DCF=![]() ∠BCD;(2)EF=CF;(3)S△CDF=S△CEF;(4)∠DFE=3∠AEF.其中正确结论的个数是( )
∠BCD;(2)EF=CF;(3)S△CDF=S△CEF;(4)∠DFE=3∠AEF.其中正确结论的个数是( )
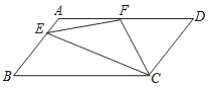
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为![]() 的网格中,点
的网格中,点![]() ,
, ![]() ,
, ![]() 均在格点上.
均在格点上.

(Ⅰ)![]() 的面积等于____________;
的面积等于____________;
(Ⅱ)若四边形![]() 是正方形,且点
是正方形,且点![]() ,
, ![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,请在如图所示的网格中,用无刻度的直尺,画出点
上,请在如图所示的网格中,用无刻度的直尺,画出点![]() ,点
,点![]() ,并简要说明点
,并简要说明点![]() ,点
,点![]() 的位置是如何找到的(不要求证明)_____________.
的位置是如何找到的(不要求证明)_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲船逆水,静水速度为28海里/时;乙船顺水,静水速度为12海里/时,两船相距60海里.已知水流速度为3海里/时,两船同时相向而行.
(1)两船同时航行1小时,求此时两船之间的距离;
(2)再(1)的情况下,两船再继续航行1小时,求此时两船之间的距离;
(3)求两船从开始航行到两船相距12海里,需要多长时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):![]() .问:
.问:
(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B.图②是点F运动时,△FBC的面积y(cm![]() )随时间x(s)变化的关系图象,则a的值是__
)随时间x(s)变化的关系图象,则a的值是__
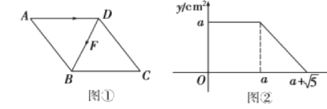
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com