
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
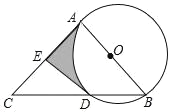
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,∠B=45°,AC=4,求图中阴影部分的面积.
【答案】(1)见解析;(2)4π
【解析】
(1)根据切线的定义可知∠CAB=90°,有圆周角定理可知∠ADB=90°,E为斜边中点
(2)阴影部分的面积等于正方形AEDO的面积减去扇形AOD的面积.
(1)如图,连接AD,OD
∵AB是直径
∴∠ADB=90°
∴∠OAD=∠ODA,∠ODB=∠OBD
∠ADE=∠EAD,∠EDC=∠ECD
∵∠EAD+∠OAD=90°
∴∠ADE+∠ODA=90°
∴直线DE与⊙O相切
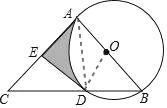
(2)由(1)可知△ACD与△ADB是直角三角形
若∠B=45°,则AC=AB=4,AE=EC=AO=DO=BO=2
∴四边形AEDO为正方形
阴影面积=正方形AEDO扇形AOD=![]() =4π
=4π


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn﹣1Bn都为等腰直角三角形(点B0是坐标原点),则△A2014B2013B2014腰长等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=x+2的图象分别交x轴,y轴于A、B两点,⊙O1过以OB为边长的正方形OBCD的四个顶点,两动点P、Q同时从点A出发在四边形ABCD上运动,其中动点P以每秒![]() 个单位长度的速度沿A→B→A运动后停止;动点Q以每秒2个单位长度的速度沿A→O→D→C→B运动,AO1交y轴于E点,P、Q运动的时间为t(秒).
个单位长度的速度沿A→B→A运动后停止;动点Q以每秒2个单位长度的速度沿A→O→D→C→B运动,AO1交y轴于E点,P、Q运动的时间为t(秒).
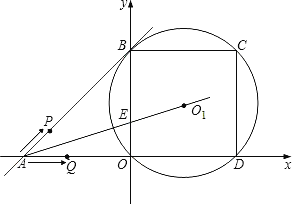
(1)求E点的坐标和S△ABE的值;
(2)试探究点P、Q从开始运动到停止,直线PQ与⊙O1有哪几种位置关系,并求出对应的运动时间t的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
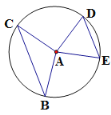
【题目】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则圆心A到弦BC的距离等于( )
A.![]() B.
B.![]() C.4D.3
C.4D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
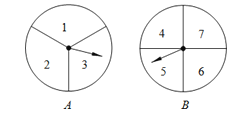
【题目】甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
(1)用列表格或画树状图的方法表示游戏所有可能出现的结果.
(2)求甲、乙两人获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
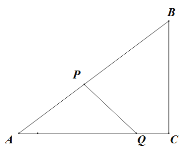
【题目】如图,在Rt△ABC中,∠C=90°,AB=10,BC=6.点P从点A出发,沿折线AB—BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动.点Q从点C出发,沿CA方向以每秒2个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
(1)求线段AC的长.
(2)求线段BP的长.(用含t的代数式表示)
(3)设△APQ的面积为S,求S与t之间的函数关系式.
(4)连结PQ,当PQ与△ABC的一边平行或垂直时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
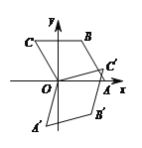
【题目】如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=4,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )
A. (2![]() ,﹣2
,﹣2![]() )B. (
)B. (![]() ,-
,-![]() )C. (2,﹣2)D. (
)C. (2,﹣2)D. (![]() ,-
,-![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹)
(2)求残片所在圆的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com