
【题目】如图,![]() 中,
中,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿折线
个单位长度的速度沿折线![]() 运动(回到点
运动(回到点![]() 停止运动),设运动时间为
停止运动),设运动时间为![]() 秒.
秒.
(1)当点![]() 在
在![]() 上时,且满足
上时,且满足![]() 时,求出此时
时,求出此时![]() 的值;
的值;
(2)当点![]() 在
在![]() 上时,求出
上时,求出![]() 为何值时,
为何值时,![]() 为以
为以![]() 为腰的等腰三角形.
为腰的等腰三角形.

【答案】(1)![]() ;(2)
;(2)![]() 秒或
秒或![]() 秒
秒
【解析】
(1)根据勾股定理可得,AC=3,根据题意可知,PA=PB=AC+CB-t=7-t,PC=t-3,根据勾股定理列关于t的方程,解方程即可得到t的值;
(2)若点P在AB上,根据运动的路程易得t的值,当AP=AC=3时,△ACP为等腰三角形,根据等量关系列出关于t的方程即可求出t的值;当CP=AC时,过点![]() 作
作![]() 于点
于点![]() 根据直角三角形面积公式可得CD的长,由勾股定理可得AD的长,根据等腰三角形的性质可得AP的长,根据等量关系列出关于t的方程即可求出t的值.
根据直角三角形面积公式可得CD的长,由勾股定理可得AD的长,根据等腰三角形的性质可得AP的长,根据等量关系列出关于t的方程即可求出t的值.
解:![]() 在
在![]() 中,
中,![]()
![]() 由勾股定理,得
由勾股定理,得![]()
如图1,连接![]()
当![]() 时,
时,![]()
在![]() 中,
中,![]()
即![]()
解得![]()
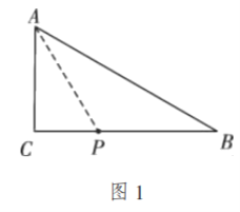
![]() ①如图2,当
①如图2,当![]() 时,
时,![]() 为等腰三角形,
为等腰三角形,
![]()
![]()
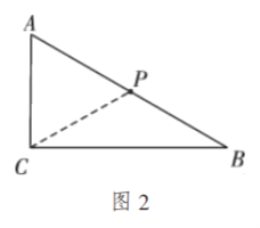
②如图3,当点![]() 在
在![]() 上,
上,![]() 时,
时,
过点![]() 作
作![]() 于点
于点![]()
![]()
![]()
![]()
在![]() 中
中
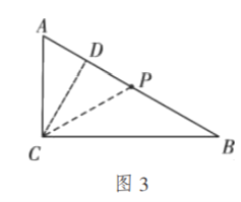
由勾股定理,得
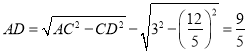
![]()
![]()
![]()
综上所述,当点![]() 在
在![]() 上,
上,![]() 为
为![]() 秒或
秒或![]() 秒时,
秒时,![]() 为以
为以![]() 为腰的等腰三角形
为腰的等腰三角形


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A、B,C三点的坐标分别为(0,1)、(3,3)、(4,0).
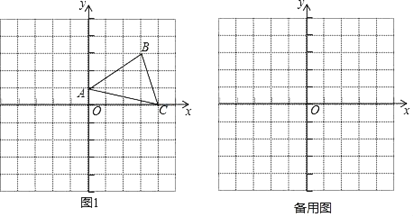
(I)S△AOC= ;
(2)若点P(m﹣1,1)是第二象限内一点,且△AOP的面积不大于△ABC的面积,求m的取值范围;
(3)若将线段AB向左平移1个单位长度,点D为x轴上一点,点E(4,n)为第一象限内一动点,连BE、CE、AC,若△ABD的面积等于由AB、BE、CE、AC四条线段围成图形的面积,则点D的坐标为 .(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,FC⊥CD,∠1=∠2,∠B=60°.

(1)求∠BCF的度数;(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
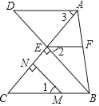
【题目】如图,BE⊥AC与点E,MN⊥AC于点N,∠1=∠2,∠3=∠C,若∠AFE=80°,求∠DAF的度数.请根据解题过程“填空”或“说明理由”.
解:∵BE⊥AC,MN⊥AC
∴BE∥MN
∴∠1= ( )
又∵∠1=∠2
∴∠2= ( )
∴EF∥BC( )
∵∠3=∠C
∴AD∥BC
∴AD∥EF
∴∠DAF+∠AFE=180°( )
∴∠DAF=180°﹣∠AFE=180°﹣80°=100°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( ) 
A.55°
B.70°
C.125°
D.145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() =(1+
=(1+![]() )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把部分a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把部分a+b![]() 的式子化为平方式的方法。
的式子化为平方式的方法。
请我仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分别表示a、b,得a=________, b=___________.
)2,用含m、n的式子分别表示a、b,得a=________, b=___________.
(2)若a+4![]() =(m+n
=(m+n![]() )2,且a、m、n均为正整数,求a的值。
)2,且a、m、n均为正整数,求a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西省平遥县政府为进一步挖掘“双林寺、老醯水镇、平遥古城”的旅游 价值,计划在2019年开工建设一条途经平遥高铁站、双林寺、老醯(读![]() ,醋的意思) 水镇、平遥古城的“旅游+交通”融合轨道观光线.甲、乙两个工程队计划参与工程建设,若让甲队单独施工
,醋的意思) 水镇、平遥古城的“旅游+交通”融合轨道观光线.甲、乙两个工程队计划参与工程建设,若让甲队单独施工![]() 天完成该项工程的
天完成该项工程的![]() ,然后乙队加入,两队还需共同施工
,然后乙队加入,两队还需共同施工![]() 天,才能完成该项工程.
天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若先让甲队施工且甲队参与该项工程施工的时间不超过![]() 天,则乙队加入后至 少要施工多少天才能完成该项工程?
天,则乙队加入后至 少要施工多少天才能完成该项工程?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com