
【题目】如图1,在平面直角坐标系中,A、B,C三点的坐标分别为(0,1)、(3,3)、(4,0).
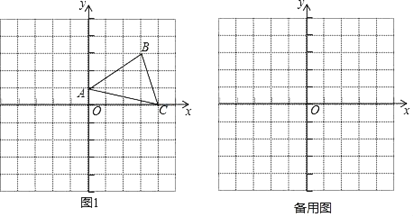
(I)S△AOC= ;
(2)若点P(m﹣1,1)是第二象限内一点,且△AOP的面积不大于△ABC的面积,求m的取值范围;
(3)若将线段AB向左平移1个单位长度,点D为x轴上一点,点E(4,n)为第一象限内一动点,连BE、CE、AC,若△ABD的面积等于由AB、BE、CE、AC四条线段围成图形的面积,则点D的坐标为 .(用含n的式子表示)
【答案】(1)2;(2)﹣10≤m<1;(3)(![]() +4,0)或(﹣
+4,0)或(﹣![]() ﹣9,0)
﹣9,0)
【解析】
(1)求出OA、OC即可解决问题;
(2)求出△ABC的面积,根据不等式即可解决问题;
(3)如图2中,延长BA交x轴于K,连接BC.首先求出直线AB的解析式,可得点K坐标,根据S△ABD=S四边形ABEC,可得S△BKD﹣S△AKD=S△BCK+S△BCE﹣S△ACK,由此构建方程即可解决问题;
解:(1)∵A(0,1),C(4,0),
∴OA=1,OC=4,
∴![]()
故答案为2.
(2)如图1,作BH⊥y轴于H.
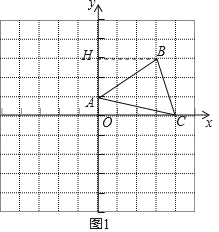
S△ABC=S四边形OCBH﹣S△ABH﹣S△OAC
![]()
![]()
由题意, ![]()
∴m≥﹣10,
∵P在第二象限,
∴m﹣1<0,
∴m<1,
∴﹣10≤m<1.
(3)如图2中,延长BA交x轴于K,连接BC.
∵A(﹣1,1),B(2,3),
设直线AB的解析式为y=kx+b,则有![]()
解得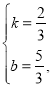
∴直线AB的解析式为![]()
∴![]() 当点D在K的右边,设D(m,0),
当点D在K的右边,设D(m,0),
∵S△ABD=S四边形ABEC,
∴S△BKD﹣S△AKD=S△BCK+S△BCE﹣S△ACK,
∴![]()
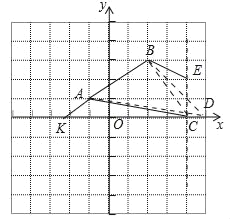
解得![]()
∴![]()
根据对称性可知,当点D′在K的左侧时,D′K=DK,可得![]()
综上所述,满足条件的D的坐标![]() 或
或![]()
方法二:当点D在K的右边,设D(m,0),(m>4),
∵![]()
S四边形ABEC=S△ABC+S△BCE![]()
![]() 解得
解得![]() 接下来同上面.
接下来同上面.
故答案为:![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°)如图①摆放,点D为AB的中点,DE交AC于点P,DF经过点C.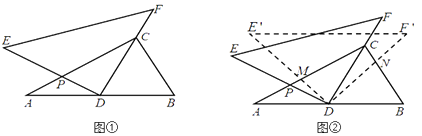
(1)求∠ADE的度数;
(2)如图②,将△DEF绕点D顺时针方向旋转角 ![]() ,此时等腰直角三角尺记为
,此时等腰直角三角尺记为 ![]() ,
, ![]() 交AC于点M,
交AC于点M, ![]() 交BC于点N,试判断
交BC于点N,试判断 ![]() 的值是否随着
的值是否随着 ![]() 的变化而变化?如果不变,请求出
的变化而变化?如果不变,请求出 ![]() 的值;反之,请说明理由.
的值;反之,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的顶点A、B的坐标分别是A(﹣1,0),B(0,﹣2),顶点C、D在双曲线y= ![]() 上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= .
上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(﹣1,0)与点C(x2 , 0),且与y轴交于点B(0,﹣2),小强得到以下结论:①0<a<2;②﹣1<b<0;③c=﹣1;④当|a|=|b|时x2> ![]() ﹣1;以上结论中正确结论的序号为 .
﹣1;以上结论中正确结论的序号为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山东全省2016年国庆假期旅游人数增长12.5%,其中尤其是乡村旅游最为火爆.泰山脚下的某旅游村,为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出,若每张床位每天收费提高20元,则相应的减少了10张床位租出,如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A.140元
B.150元
C.160元
D.180元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,沿
,沿![]() 将
将![]() 折叠,得
折叠,得![]() .
.
(1)如图所示,当![]() 时,
时,![]() _______度;
_______度;

(2)如图所示,当![]() 时,求线段
时,求线段![]() 的长度;
的长度;

(3)当点![]() 为
为![]() 中点时,点
中点时,点![]() 是边
是边![]() 上不与点
上不与点![]() 、
、![]() 重合的一个动点,将
重合的一个动点,将![]() 沿
沿![]() 折叠,得到
折叠,得到![]() ,连接
,连接![]() ,求
,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )

A.①②B.②③C.①③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿折线
个单位长度的速度沿折线![]() 运动(回到点
运动(回到点![]() 停止运动),设运动时间为
停止运动),设运动时间为![]() 秒.
秒.
(1)当点![]() 在
在![]() 上时,且满足
上时,且满足![]() 时,求出此时
时,求出此时![]() 的值;
的值;
(2)当点![]() 在
在![]() 上时,求出
上时,求出![]() 为何值时,
为何值时,![]() 为以
为以![]() 为腰的等腰三角形.
为腰的等腰三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com