
【题目】将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°)如图①摆放,点D为AB的中点,DE交AC于点P,DF经过点C.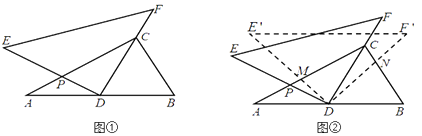
(1)求∠ADE的度数;
(2)如图②,将△DEF绕点D顺时针方向旋转角 ![]() ,此时等腰直角三角尺记为
,此时等腰直角三角尺记为 ![]() ,
, ![]() 交AC于点M,
交AC于点M, ![]() 交BC于点N,试判断
交BC于点N,试判断 ![]() 的值是否随着
的值是否随着 ![]() 的变化而变化?如果不变,请求出
的变化而变化?如果不变,请求出 ![]() 的值;反之,请说明理由.
的值;反之,请说明理由.
【答案】
(1)解:∵∠ACB=90°,点D为AB的中点,
∴CD=AD=BD= ![]() AB,
AB,
∴∠ACD=∠A=30°,
∴∠ADC=180°-30°×2=120°,
∴∠ADE=∠ADC-∠EDF=120°-90°=30°
(2)解:不变化.
∵∠EDF=90°,
∴∠PDM+∠E′DF=∠CDN+∠E′DF=90°,
∴∠PDM=∠CDN,
∵∠B=60°,BD=CD,
∴△BCD是等边三角形,
∴∠BCD=60°,
∵∠CPD=∠A+∠ADE=30°+30°=60°,
∴∠CPD=∠BCD,
在△DPM和△DCN中,![]() ,
,
∴△DPM∽△DCN,
∴ ![]() ,
,
∵ ![]() =tan∠ACD=tan30°=
=tan∠ACD=tan30°= ![]() ,
,
∴ ![]() 的值不随着α的变化而变化,是定值
的值不随着α的变化而变化,是定值 ![]()
【解析】先根据直角三角形斜边上的中线性质得CD=AD=DB,则∠ACD=∠A=30°,∠BCD=∠B=60°,由于∠EDF=90°,可利用互余得∠CPD=60°,再根据旋转的性质得∠PDM=∠CDN=α,于是可判断△PDM∽△CDN,然后在Rt△PCD中利用正切的定义得到tan∠PCD=tan30°的值,于是可得结论。


科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 是角平分线,
是角平分线,![]() 是
是![]() 上的点,
上的点, ![]() 相交于点
相交于点![]() .
.
(1) 如图2,若![]() =90°,求证:
=90°,求证: ![]()
![]() ;
;
(2) 如图1,若![]() =
=![]() ( 0°<
( 0°< ![]() <180°).
<180°).
①求![]()
![]() 的值(用含
的值(用含![]() 的代数式表示);
的代数式表示);
②是否存在![]() ,使
,使![]() 小于
小于![]() ,如果存在,求出
,如果存在,求出![]() 的范围,如果不存在,请说明理由.
的范围,如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线相交于点A1,得∠A1;∠A1BC和∠A1CD的平分线相交于点A2,得∠A2;…;∠A2018BC和∠A2018CD的平分线交于点A2019,则∠A2019=________度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年是大家公认的![]() 商用元年.移动通讯行业人员想了解
商用元年.移动通讯行业人员想了解![]() 手机的使用情况,在某高校随机对500位大学生进行了问卷调查.下列说法正确的是( )
手机的使用情况,在某高校随机对500位大学生进行了问卷调查.下列说法正确的是( )
A.该调查方式是普查
B.该调查中的个体是每一位大学生
C.该调查中的样本是被随机调查的500位大学生![]() 手机的使用情况
手机的使用情况
D.该调査中的样本容量是500位大学生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1560元,20本文学名著比20本动漫书多360元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于74本,总费用不超过2100,请求出所有符合条件的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两点在反比例函数y= ![]() 的图象上,C,D两点在反比例函数y=
的图象上,C,D两点在反比例函数y= ![]() 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1﹣k2的值是( )
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1﹣k2的值是( ) 
A.6
B.4
C.3
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A、B,C三点的坐标分别为(0,1)、(3,3)、(4,0).
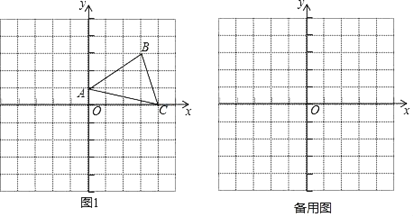
(I)S△AOC= ;
(2)若点P(m﹣1,1)是第二象限内一点,且△AOP的面积不大于△ABC的面积,求m的取值范围;
(3)若将线段AB向左平移1个单位长度,点D为x轴上一点,点E(4,n)为第一象限内一动点,连BE、CE、AC,若△ABD的面积等于由AB、BE、CE、AC四条线段围成图形的面积,则点D的坐标为 .(用含n的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com