
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,沿
,沿![]() 将
将![]() 折叠,得
折叠,得![]() .
.
(1)如图所示,当![]() 时,
时,![]() _______度;
_______度;

(2)如图所示,当![]() 时,求线段
时,求线段![]() 的长度;
的长度;

(3)当点![]() 为
为![]() 中点时,点
中点时,点![]() 是边
是边![]() 上不与点
上不与点![]() 、
、![]() 重合的一个动点,将
重合的一个动点,将![]() 沿
沿![]() 折叠,得到
折叠,得到![]() ,连接
,连接![]() ,求
,求![]() 周长的最小值.
周长的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)求出![]() ,利用翻折不变性解决问题即可.
,利用翻折不变性解决问题即可.
(2)如图2中,作BH⊥AD于H.根据30度角所对的直角边等于斜边的一半及勾股定理求出AH,PH即可解决问题.
(3)![]() 的周长=
的周长=![]() +BF+
+BF+![]() =AF+BF+
=AF+BF+![]() =AB+
=AB+![]() =10+
=10+![]() ,推出当
,推出当![]() 的周长最小时,
的周长最小时,![]() 的周长最小,由此即可解决问题.
的周长最小,由此即可解决问题.
(1)如图1:
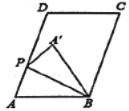
图1
∵![]()
∴![]()
由折叠的性质可知:
![]()
故答案为:![]()
(2)如图2:作BH⊥AD于H
在Rt△ABH中
∵∠AHB=![]() ,AB=10,
,AB=10,![]()
∴∠ABH=![]()
∴AH=![]() AB=5
AB=5
![]() BH=
BH=![]()
∵四边形ABCD是平行四边形
∴AD∥BC
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
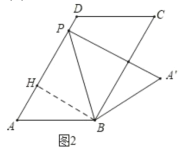
故答案为:![]()
(3)如图3中,作BH⊥AD于H ,连接BP
∵PA=8,AH=5
∴PH=3
∵BH=![]()
∴PB=![]()
由翻折可知:PA=![]() =8,FA=
=8,FA=![]() ,
,
![]() 的周长
的周长
![]() +BF+
+BF+![]() =AF+BF+
=AF+BF+![]() =AB+
=AB+![]() =10+
=10+![]()
∴当![]() 最小时,
最小时, ![]() 的周长最小
的周长最小
∵![]()
∴![]()
∴![]() 的最小值为
的最小值为![]()
∴![]() 的周长的最小值为:
的周长的最小值为: ![]()
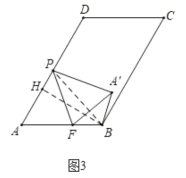
故答案为:![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:小明遇到这样一个问题;△ABC中,有两个内角相等.
①若∠A=110°,求∠B的度数;
②若∠A=40°,求∠B的度数.
小明通过探究发现,∠A的度数不同,∠B的度数的个数也可能不同,因此为同学们提供了如下解题的想法:
对于问题①,根据三角形内角和定理,∵∠A=110°>90°,∠B=∠C=35°;
对于问题②,根据三角形内角和定理,∵∠A=40°<90°,∴∠A=∠B或∠A=∠C或∠B=∠C,∴∠B的度数可求.请回答:
(1)问题②中∠B的度数为 ;
(2)参考小明解决问题的思路,解决下面问题:
△ABC中,有两个内角相等.设∠A=x°,当∠B有三个不同的度数时,求∠B的度数(用含x的代式表示)以及x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A、B,C三点的坐标分别为(0,1)、(3,3)、(4,0).
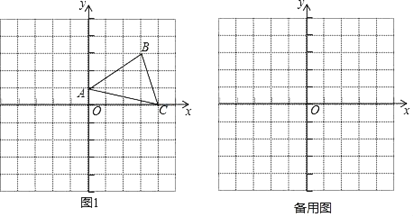
(I)S△AOC= ;
(2)若点P(m﹣1,1)是第二象限内一点,且△AOP的面积不大于△ABC的面积,求m的取值范围;
(3)若将线段AB向左平移1个单位长度,点D为x轴上一点,点E(4,n)为第一象限内一动点,连BE、CE、AC,若△ABD的面积等于由AB、BE、CE、AC四条线段围成图形的面积,则点D的坐标为 .(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市“精准扶贫”工作中,甲、乙两个工程队先后接力为扶贫村庄修建一条210米长的公路,甲队每天修建15米,乙队每天修建25米,一共用10天完成.
根据题意,小红和小芳同学分别列出了下面尚不完整的方程组:
小红:![]() 小芳:
小芳:
(1)请你分别写出小红和小芳所列方程组中未知数x,y表示的意义:
小红:x表示______,y表示______;
小芳:x表示______,y表示______;
(2)在题中“( )”内把小红和小芳所列方程组补充完整;
(3)甲工程队一共修建了______天,乙工程队一共修建了______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个直角三角形纸板ABC放置在锐角△PMN上,使该直角三角形纸板的两条直角边AB,AC分别经过点M,N.
(发现)
(1)如图1,若点A在△PMN内,当∠P=30°时,则∠PMN+∠PNM=______°,∠AMN+∠ANM=______°,∠PMA+∠PNA=______°.
(2)如图2,若点A在△PMN内,当∠P=50°时,∠PMA+∠PNA=______°.
(探究)
(3)若点A在△PMN内,请你判断∠PMA,∠PNA和∠P之间满足怎样的数量关系,并写出理由.
(应用)
(4)如图3,点A在△PMN内,过点P作直线EF∥AB,若∠PNA=16°,则∠NPE=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件工艺品的进价为100元,标价135元出售,每天可售出100件,根据销售统计,一件工艺品每降价1元,则每天可多售出4件,要使每天获得的利润最大,则每件需降价( )
A.3.6 元
B.5 元
C.10 元
D.12 元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,FC⊥CD,∠1=∠2,∠B=60°.

(1)求∠BCF的度数;(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() =(1+
=(1+![]() )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把部分a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把部分a+b![]() 的式子化为平方式的方法。
的式子化为平方式的方法。
请我仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分别表示a、b,得a=________, b=___________.
)2,用含m、n的式子分别表示a、b,得a=________, b=___________.
(2)若a+4![]() =(m+n
=(m+n![]() )2,且a、m、n均为正整数,求a的值。
)2,且a、m、n均为正整数,求a的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com