
【题目】阅读下面材料:小明遇到这样一个问题;△ABC中,有两个内角相等.
①若∠A=110°,求∠B的度数;
②若∠A=40°,求∠B的度数.
小明通过探究发现,∠A的度数不同,∠B的度数的个数也可能不同,因此为同学们提供了如下解题的想法:
对于问题①,根据三角形内角和定理,∵∠A=110°>90°,∠B=∠C=35°;
对于问题②,根据三角形内角和定理,∵∠A=40°<90°,∴∠A=∠B或∠A=∠C或∠B=∠C,∴∠B的度数可求.请回答:
(1)问题②中∠B的度数为 ;
(2)参考小明解决问题的思路,解决下面问题:
△ABC中,有两个内角相等.设∠A=x°,当∠B有三个不同的度数时,求∠B的度数(用含x的代式表示)以及x的取值范围.
【答案】(1)40°或70°或100°;(2)∠B=x°或180°﹣2x°或90°﹣![]() x°,x的取值范围是0<x<90且x≠60.
x°,x的取值范围是0<x<90且x≠60.
【解析】
(1)根据三角形内角和定理即可求出答案.
(2)由(1)问的解答过程可类比求出x的取值范围.
解:(1)当∠A=∠B时,
∴∠B=40°,
当∠A=∠C=40°时,
∴∠B=180﹣∠A﹣∠C=100°,
当∠B=∠C时,
∴![]()
故∠B的度数为40°或70°或100°
(2)当0<x<90时,∠B的度数有三个,
当∠A=∠B时,∠B=x°,
当∠A=∠C时,
∵∠A+∠B+∠C=180°,
∴∠B=180﹣2x°,
当∠B=∠C时,
∵∠A+∠B+∠C=180°,
∴![]()
∵![]()
∴x≠60
∴∠B=x°或180°﹣2x°或![]()
x的取值范围是0<x<90且x≠60


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】如图①所示,已知,BC∥OA,∠B=∠A=100°,试解答下列问题:
(1)试说明:OB∥AC;

(2)如图②,若点E.F在BC上,且∠FOC=∠AOC,OE平分∠BOF.试求∠EOC的度数;

(3)在(2)小题的条件下,若左右平行移动AC,如图③,那么∠OCB:∠OFB的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.

(4)在(3)小题的条件下,当∠OEB=∠OCA时,试求∠OCA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数y= ![]() 的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )
的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )
A.y=﹣ ![]()
B.y=﹣ ![]()
C.y=﹣ ![]()
D.y= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的顶点A、B的坐标分别是A(﹣1,0),B(0,﹣2),顶点C、D在双曲线y= ![]() 上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= .
上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的中线,E,F为直线AD上的点,连接BE,CF,且BE∥CF.
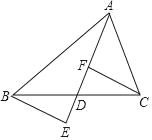
(1)求证:DE=DF;
(2)若在原有条件基础上再添加AB=AC,你还能得出什么结论.(不用证明)(写2个)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(﹣1,0)与点C(x2 , 0),且与y轴交于点B(0,﹣2),小强得到以下结论:①0<a<2;②﹣1<b<0;③c=﹣1;④当|a|=|b|时x2> ![]() ﹣1;以上结论中正确结论的序号为 .
﹣1;以上结论中正确结论的序号为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,沿
,沿![]() 将
将![]() 折叠,得
折叠,得![]() .
.
(1)如图所示,当![]() 时,
时,![]() _______度;
_______度;

(2)如图所示,当![]() 时,求线段
时,求线段![]() 的长度;
的长度;

(3)当点![]() 为
为![]() 中点时,点
中点时,点![]() 是边
是边![]() 上不与点
上不与点![]() 、
、![]() 重合的一个动点,将
重合的一个动点,将![]() 沿
沿![]() 折叠,得到
折叠,得到![]() ,连接
,连接![]() ,求
,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com