
如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是 ( )
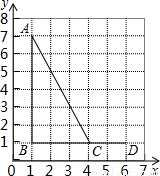
A.(6,0) B.(6,3) C.(6,5) D.(4,2)
B.
【解析】
试题分析:△ABC中,∠ABC=90°,AB=6,BC=3,AB:BC=2.
A、当点E的坐标为(6,0)时,∠CDE=90°,CD=2,DE=1,则AB:BC=CD:DE,△CDE∽△ABC,故本选项不符合题意;
B、当点E的坐标为(6,3)时,∠CDE=90°,CD=2,DE=2,则AB:BC≠CD:DE,△CDE与△ABC不相似,故本选项符合题意;
C、当点E的坐标为(6,5)时,∠CDE=90°,CD=2,DE=4,则AB:BC=DE:CD,△EDC∽△ABC,故本选项不符合题意;
D、当点E的坐标为(4,2)时,∠ECD=90°,CD=2,CE=1,则AB:BC=CD:CE,△DCE∽△ABC,故本选项不符合题意;
故选:B.
考点:1.相似三角形的判定;2.坐标与图形性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年山东省九年级上学期期末调研数学试卷(解析版) 题型:填空题
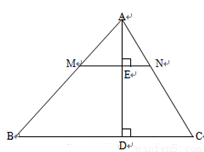
如图,AD是△ABC的高,点M在AB边上,点N在AC边上,MN⊥AD,垂足为E.下列说法正确的是 .(只填序号)
①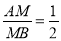 ,则
,则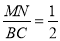 ;
;
②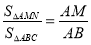 ;
;
③若△AMN与△ABC的相似比是2:3,且△AMN的周长为6,则△ABC的周长为9;
④若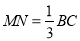 ,则
,则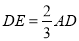 .
.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:选择题
已知抛物线y=x2﹣2x+m+1与x轴有两个不同的交点,则函数y=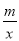 的大致图象是( )
的大致图象是( )
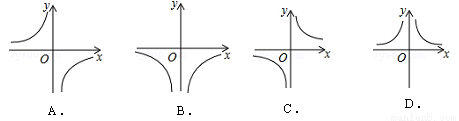
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市林甸县九年级上学期期末检测数学试卷(解析版) 题型:解答题
小明对自己所在班级的50名学生平均每周参加课外活动的时间进行了调查,由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
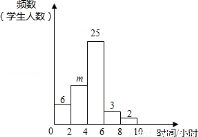
(1)求m的值;
(2)从参加课外活动时间在6~10小时的5名学生中随机选取2人,请你用列表或画树状图的方法,求其中至少有1人课外活动时间在8~10小时的概率.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市林甸县九年级上学期期末检测数学试卷(解析版) 题型:填空题
小明家离学校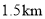 ,小明步行上学需
,小明步行上学需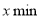 ,那么小明步行速度
,那么小明步行速度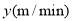 可以表示为
可以表示为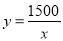 ;水平地面上重
;水平地面上重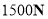 的物体,与地面的接触面积为
的物体,与地面的接触面积为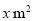 ,那么该物体对地面压强
,那么该物体对地面压强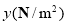 可以表示为
可以表示为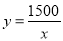 ;
;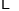 ,函数关系式
,函数关系式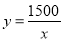 还可以表示许多不同情境中变量之间的关系,请你再列举1例: .
还可以表示许多不同情境中变量之间的关系,请你再列举1例: .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市林甸县九年级上学期期末检测数学试卷(解析版) 题型:选择题
已知一次函数y1=kx+b(k<0)与反比例函数y2=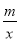 (m≠0)的图象相交于A、B两点,其横坐标分别是-1和3,当y1>y2时,实数x的取值范围是( )
(m≠0)的图象相交于A、B两点,其横坐标分别是-1和3,当y1>y2时,实数x的取值范围是( )
A.x<-l或0<x<3 B.一1<x<0或0<x<3
C.一1<x<0或x>3 D.0<x<3
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省长汀县城区三校九年级12月联考数学试卷(解析版) 题型:解答题
(14分)如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.
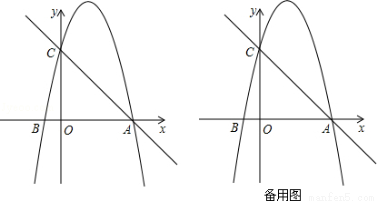
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得∠PCO=∠POC?若存在,求出符合条件的点P的坐标;若不存在,说明理由;
(3)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省七年级上学期期末调研数学试卷(解析版) 题型:解答题
(本题满分8分)
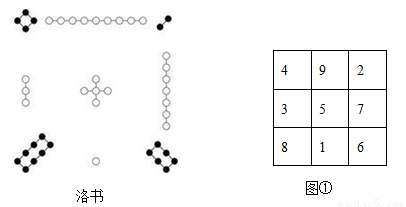
“洛书”简介:
“洛书”是世界上最古老的一个三阶幻方,它有3行3列,三横行的三个数之和,三竖列的三个数之和,两对角线的三个数之和都等于15.其实幻方就是把一些有规律的数填在纵横格数都相等的正方形图内,使每一行、每一列和每一条对角线上各个数之和都相等.
问题发现:
“洛书”中还有一些规律是可以总结的,如:
(1)在“洛书”中放在最中间的数5称为核心数,这个数的确定不是随便填上去的,是有一定方法可寻的,那么请你在图①中写出一条寻找核心数的方法.
(2)如果把图①中每一列三个数(从上到下)看做一个三位数,则这三个三位数之和等于它们的逆转数(从下到上)之和.
验证:每一列三个数(从上到下)组成的三位数之和即:438+951+276=1665,它们的逆转数(从下到上)三个三位数之和:834+159+672=1665.
依据上面的发现,你能提出什么样的问题?并验证你所提出的问题.
提出问题:
验证:
问题拓展:
怎样的九个数能构造成三阶幻方呢?
(1)将洛书中的九个数分别加上1可得:2,3,4,5,6,7,8,9,10.它们能否构造成一个三阶幻方?如果能,请在图②的格子中写出一种排列法.
(2)请你写一个能构成三阶幻方的九个数(区别于上述所举的数):
(3)请你总结一个一般性的结论:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com