
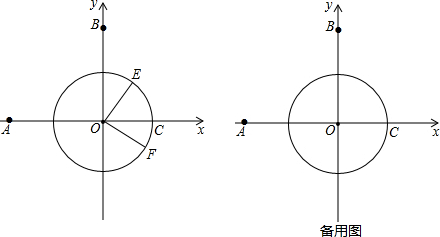
分析 (1)已知了抛物线上A,B,C三点的坐标,可用待定系数法求出抛物线的解析式;
(2)点F是⊙O 上的一动点,根据其运动规律,点F(a,b)(a>0),点E在第一,二象限,若F按逆时针运动,∠EAO在逐渐增大,当运动至与过点A的切线的切点重合时,∠EAO=30°,∠EAO最大,存在着点F(a,b)(a>0),使得∠EAO=28°;
(3)根据变化规律,不难发现当点D与点M重合时,点D的纵坐标y最大,利用勾股定理即可得到结果;
(4)当点F在x轴的负半轴时,点E在y轴的负半轴时,n值最小,直线AE与直线BF解析式求出交点坐标,求的n=-$\frac{2}{5}$;当点F在x轴的正半轴时,点E在y轴的正半轴,此时n值最大,n=$\frac{6}{5}$,∴$-\frac{2}{5}$≤n≤$\frac{6}{5}$
解答 解:(1)设该抛物线的解析式为:y=ax2+bx+c,
将A(-2,0),B(0,2),C(1,0)代入得,
$\left\{\begin{array}{l}{0=4a-2b+c}\\{2=c}\\{0=a+b+c}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-1}\\{b=-1}\\{c=2}\end{array}\right.$,
∴该抛物线的解析式为:y=-x2-x+2;
(2)存在.证明:点F(a,b)(a>0),
点E在第一,二象限,若F按逆时针运动,
∠EAO在逐渐增大,
过点A做⊙O的切线⊙O于点M,
E点与M点重合时,AO=2,OE=1,
∴∠EAO=30°,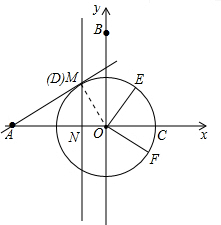
∴存在着点F(a,b)(a>0),使得∠EAO=28°;
(3)如图,抛物线对称轴为x=-$\frac{1}{2}$,
直线x=$-\frac{1}{2}$与圆相交于点M,
当点D与点M重合时,
点D的纵坐标y最大为:
y=MN=$\sqrt{{OM}^{2}{-ON}^{2}}$=$\sqrt{\frac{3}{4}}$=$\frac{\sqrt{3}}{2}$,
∴y最大值为:$\frac{\sqrt{3}}{2}$;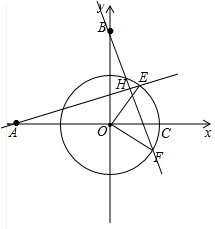 (4)当点F在x轴的负半轴时,点E在y轴的负半轴时,F(-1,0),E(0,-1),
(4)当点F在x轴的负半轴时,点E在y轴的负半轴时,F(-1,0),E(0,-1),
设直线AE解析式为:y=kx+b,代入得$\left\{\begin{array}{l}{0=-2k+b}\\{-1=b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-1}\end{array}\right.$,
∴直线AE解析式为:y=-$\frac{1}{2}x$-1,
设直线BF解析式为:y=kx+b,代入得:$\left\{\begin{array}{l}{2=b}\\{0=-k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=2}\\{b=2}\end{array}\right.$,
∴直线BF解析式为:y=2x+2,
组方程组:$\left\{\begin{array}{l}{y=-\frac{1}{2}x-1}\\{y=2x+2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=-\frac{6}{5}}\\{y=-\frac{2}{5}}\end{array}\right.$即n=$-\frac{2}{5}$,此时n最小;
当点F在x轴的正半轴时,点E在y轴的正半轴时,F(1,0),E(0,1),
设直线AE解析式为:y=kx+b,代入得$\left\{\begin{array}{l}{0=-2k+b}\\{1=b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=1}\end{array}\right.$,
∴直线AE解析式为:y=$\frac{1}{2}x+1$,
设直线BF解析式为:y=kx+b,代入得:$\left\{\begin{array}{l}{2=b}\\{0=k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-2}\\{b=2}\end{array}\right.$,
∴直线BF解析式为:y=-2x+2,
组方程组:$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{y=-2x+2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=\frac{2}{5}}\\{y=\frac{6}{5}}\end{array}\right.$,即n=$\frac{6}{5}$,此时n最大,
∴$-\frac{2}{5}$≤n≤$\frac{6}{5}$.
点评 本题考查了待定系数法求解析式,变化规律,数形结合,分析变化规率是解决此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
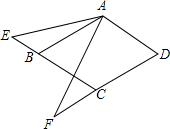 如图,菱形ABCD中,AB=a,∠ABC=60°,点E、F分别在CB、DC的延长线上,∠EAF=60°.
如图,菱形ABCD中,AB=a,∠ABC=60°,点E、F分别在CB、DC的延长线上,∠EAF=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com