
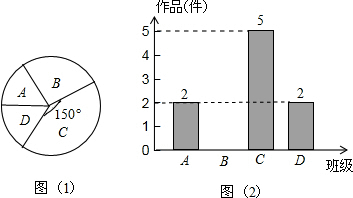
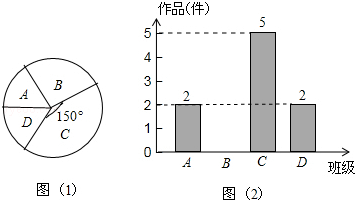
分析 (1)由题意可求得李老师所调查的4个班征集到作品共:5÷$\frac{150}{360}$=12(件),B班征集到作品:12-2-5-2=3(件);继而可补全条形统计图;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好抽中一男一女的情况,再利用概率公式即可求得答案.
解答 解:(1)∵李老师所调查的4个班征集到作品共:5÷$\frac{150}{360}$=12(件),
∴B班征集到作品:12-2-5-2=3(件);
∴李老师采取的调查方式是抽样调查,李老师所调查的4个班征集到作品共12件,其中B班征集到作品3件,
故答案为:抽样调查;12;3;
补全图2,如图所示:
(2)画树状图如下:
∵所有等可能的情况有12种,其中一男一女有8种,
∴恰好抽中一男一女的概率为:$\frac{8}{12}$=$\frac{2}{3}$.
点评 此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
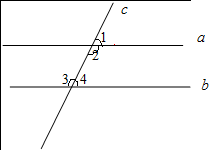 如图,因为a∥b,所以∠1=∠4,理由是两直线平行,同位角相等.
如图,因为a∥b,所以∠1=∠4,理由是两直线平行,同位角相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
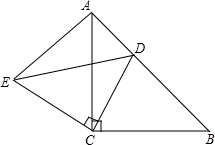 已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为线段AB上一动点.
已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为线段AB上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
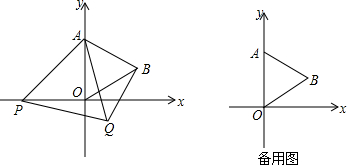
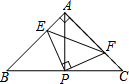 如图,在Rt△ABC中,∠BAC=90°,AB=AC,直角∠EPF的顶点P是BC的中点,将∠EPF绕顶点P旋转,两边PE,PF分别交AB,AC于点E,F.下列四个结论:
如图,在Rt△ABC中,∠BAC=90°,AB=AC,直角∠EPF的顶点P是BC的中点,将∠EPF绕顶点P旋转,两边PE,PF分别交AB,AC于点E,F.下列四个结论:| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
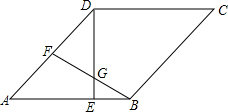 如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,DE、BF相交于点G,连接CG.
如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,DE、BF相交于点G,连接CG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com