练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

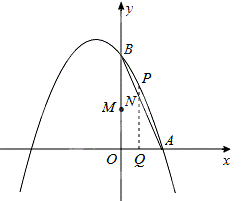
    如图，已知抛物线经过A（1，0），B（0，3），C(-3，0)三点．

    （1）求抛物线对应的函数关系式；

    （2）动点Q从点O出发，以每秒1个单位长度的速度在线段OA上运动，同时动点M从O点出发以每秒3个单位长度的速度在线段OB上运动，过点Q作x轴的垂线交线段AB于点N，交抛物线于点P，设运动的时间为t秒．

    ①当t为何值时，四边形OMPQ为矩形；

    ②△AON能否为等腰三角形？若能，求出t的值；若不能，请说明理由．




    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


              

    查看答案和解析>>

    科目：初中数学 来源： 题型：


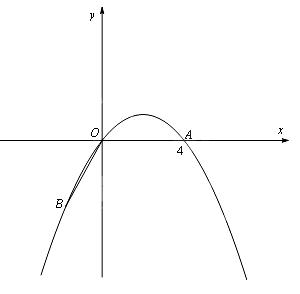
    如图，点A在x轴上，OA=4，将线段OA绕点O顺时针旋转120°至

        OB的位置.

    (1)求点B的坐标;

    (2)求过点A、O、B的抛物线的解析式;

    (3)在此抛物线的对称轴上，是否存在点P，使得以点P、O、B为顶点的三角形

       是等腰三角形？若存在，求出点P坐标；若不存在，说明理由.

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点P在双曲线y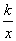＝（x＞0）上，⊙P与两坐标轴都相切，点E为y轴负半轴上的一点，过点P作PF⊥PE交x轴于点F，若OF－OE＝8，则k的值是     ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某市为了增强学生体质，全面实施“学生饮用奶”营养工程．某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用．某中学为了了解学生对不同口味牛奶的喜好，对全校订购牛奶的学生进行了随机调查（每盒各种口味牛奶的体积相同），绘制了如图两张不完整的人数统计图：

    （1）本次被调查的学生有　 　名；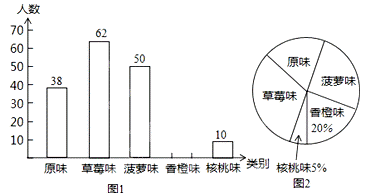

    （2）补全上面的条形统计图1，并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图2中所占圆心角的度数；

    （3）该校共有2400名学生订购了该品牌的牛奶，牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶．要使学生每天都喝到自己喜好的口味的牛奶，牛奶供应商每天送往该校的牛奶中，草莓味要比原味多送多少盒？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=3，则BC的长为（　　）

        A、1        B、2

        C、      D、

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点A是反比例函数y=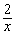(x＞0)的图象上任意一点，AB∥x轴交反比例函数y=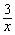－ 的图象于点B，以AB为边作□ABCD，其中C、D在x轴上，则S□ABCD为(    )

    A．2    B．3    C．4    D．5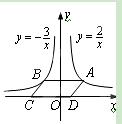

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    将一直角三角板与两边平行的纸条如图放置．已知∠1=30°，则∠2的度数为（   ）

    A．30°             B．45°             C．50°             D．60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图17，有一种动画程序，屏幕上正方形ABCD是黑色区域（含正方形边界），其中A（1，1），B（2，1），C（2，2），D（1，2），用信号枪沿直线y=﹣2x+b发射信号，当信号遇到黑色区域时，区域便由黑变白，则能够使黑色区域变白的b的取值范围为　         　．

           

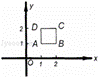
    查看答案和解析>>

    同步练习册答案