Question

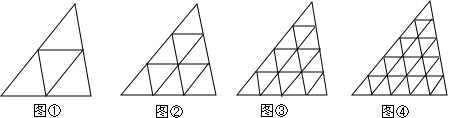
如图①，我们知道顺次连接三角形的三边中的（把三边二等分，此时等分数为2）可以吧原三角形分成4分形状与大小相同的小三角形，如果把三条边分别3等分（此时等分数为3），按图②方式将等分点连起来，可以看到整个三角形被分成了9个形状与大小相同的小三角形，…我们来研究这些形状与大小相同的小三角形个数a、顶点数b、边数c与等分数n之间的关系．

等分数n	小三角形个数a	顶点数b	边数c
2	4	6	9
3	9	10	18
4	__________	__________	__________
5	__________	__________	__________
…	…	…	…

（1）如果把三角形的各边分别4等分、5等分，并按上述的方法连接（如图③、图④所示），请将图③、图④中的小三角形个数，顶点数，边数填入上述表格中；

（2）观察上述，如果把三角形的各边分别n等分（此时等分数为n），并按上述的方法连接，形状与大小相同的小三角形个数a，顶点数b，边数c都与等分数n存在一定的关系，请用含n的代数式分别表示出来；

（3）当n=10时，分别求出小三角形个数a、顶点数b、边数c的值．

Answer 1

【考点】规律型：图形的变化类．

【分析】（1）由三角形的各边2等分，把原三角形分成4分形状与大小相同的小三角形，顶点为1+2+3=6个，边数为3×（1+2+3）=18个；三角形的各边3等分，把原三角形分成9分形状与大小相同的小三角形，顶点为1+2+3+4=10个，边数为3×（1+2+3+4）=30个；三角形的各边4等分，把原三角形分成16分形状与大小相同的小三角形，顶点为1+2+3+4+5=15个，边数为3×（1+2+3+4+5）=45个；…由此得出三角形的各边n等分，把原三角形分成n²分形状与大小相同的小三角形，顶点为1+2+3+…+n=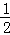n（n+1）个，边数为3×（1+2+3+…+n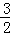）=n（n+1）个；由此计算得出答案即可；

（2）利用（1）中的规律得出答案即可；

（3）把n=10代入（2）中的规律求得答案即可．

【解答】解：（1）填表如下：

等分数n	小三角形个数a	顶点数b	边数c
2	4	6	9
3	9	10	18
4	16	15	30
5	25	21	45
…	…	…	…

（2）小三角形个数a=n²，顶点数b=1+2+3+…+n=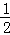n（n+1）个，边数c=3×（1+2+3+…+n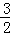）=n（n+1）个；

（3）当n=10时，小三角形个数a=100，顶点数b=55，边数c=165．

【点评】此题考查图形的变化规律，找出图形之间的联系，得出点的排列规律，利用规律解决问题．