
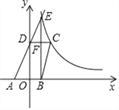
【题目】如图,已知四边形ABCD顶点A、B在x轴上,点D在y轴上,函数y=![]() (x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.
(x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.
(1)若EB=![]() OD,求点E的坐标;
OD,求点E的坐标;
(2)若四边形ABCD为平行四边形,求过A、D两点的函数关系式.
【答案】(1)(![]() ,4); (2)y=3x+3.
,4); (2)y=3x+3.
【解析】分析:(1)根据点C坐标求出反比例函数的解析式,再求出点E的纵坐标,即可解决问题.
(2)设E(m, ![]() ),则B(m,0),由四边形ABCD是平行四边形,推出CD=AB=2,由DF∥AB,推出
),则B(m,0),由四边形ABCD是平行四边形,推出CD=AB=2,由DF∥AB,推出![]() ,推出
,推出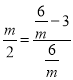 ,解得m=1,可得E(1,6),设直线AD的解析式为y=kx+b,利用待定系数法即可解决问题.
,解得m=1,可得E(1,6),设直线AD的解析式为y=kx+b,利用待定系数法即可解决问题.
本题解析:(1)∵C(2,3),
把C(2,3)代入y=![]() 中,k=6,
中,k=6,
∴y=![]() ,
,
∵CD⊥y轴,
∴OD=3,
∵BE=![]() OD,
OD,
∴BE=4,
∴y=4时,4=![]() ,
,
∴x=![]() ,
,
∴点E坐标(![]() ,4);
,4);
(2)设E(m, ![]() ),则B(m,0),
),则B(m,0),
∵四边形ABCD是平行四边形,
∴CD=AB=2,
∵DF∥AB,
∴![]() ,
,
∴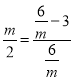 ,
,
解得m=1,
∴E(1,6),
设直线AD的解析式为y=kx+b,则有![]() ,
,
解得![]() ,
,
∴直线AD的解析式为y=3x+3.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
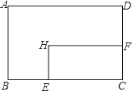
【题目】矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )
A. 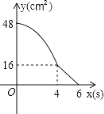 B.
B. 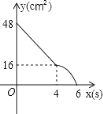 C.
C. 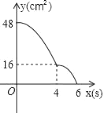 D.
D. 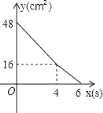
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点D,E为圆心,大于 ![]() DE的长为半径作弧,两弧交于F;
DE的长为半径作弧,两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K,使K和B在AC的两侧;
所以,BH就是所求作的高.其中顺序正确的作图步骤是( )
A.①②③④
B.④③②①
C.②④③①
D.④③①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班一个小组7名同学的体育测试成绩(满分30分)依次为:27,29,27,25,27,30,25,这组数据的中位数和众数分别是( )
A.27,25
B.25,27
C.27,27
D.27,30
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com