
 ����AB��ֱ��AB��x�ύ�ڵ�C����y�ύ�ڵ�D��ƽ������һ��E��3��1����ֱ��BE��x�ύ�ڵ�F��ֱ��AB�Ľ���ʽ����y1=kx+b��ֱ��BE����ʽ����y2=mx+t����
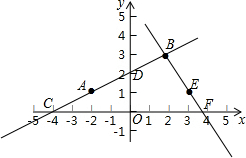
����AB��ֱ��AB��x�ύ�ڵ�C����y�ύ�ڵ�D��ƽ������һ��E��3��1����ֱ��BE��x�ύ�ڵ�F��ֱ��AB�Ľ���ʽ����y1=kx+b��ֱ��BE����ʽ����y2=mx+t�������� ��1�����ݹ۲�ͼ������ҳ���B��C��D�����꣬���ݴ���ϵ�����������ֱ��AB��BE�Ľ���ʽ����y2=0���������F�����꣬��������ε������ʽ���ɵó����ۣ�
��2����ֱ��AB��ͼ����ֱ��BEͼ���Ϸ�ʱ����kx+b��mx+t����ֱ��AB��ͼ����ֱ��BEͼ���·�ʱ����kx+b��mx+t�������ཻʱ����kx+b=mx+t�����ͼ�ɵó����ۣ�
��3�����H������Ϊ��n��0�����������ľ��빫ʽ�ҳ�OB��OH��BH�ij��ȣ���ϡ�OBHΪ���������ε�����������������n��ֵ��
��� �⣺��1���۲캯��ͼ���֪��
��C��-4��0������D��0��2������B��2��3����
��C��D���������ֱ��AB�Ľ���ʽ�У���$\left\{\begin{array}{l}{0=-4k+b}\\{2=b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$��
��ֱ��AB�Ľ���ʽΪy1=$\frac{1}{2}$x+2��
����B��2��3����E��3��1�����뵽ֱ��BE�Ľ���ʽ�У���$\left\{\begin{array}{l}{3=2m+t}\\{1=3m+t}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{m=-2}\\{t=7}\end{array}\right.$��
��ֱ��BE�Ľ���ʽΪy2=-2x+7��
��y2=0������-2x+7=0�����m=$\frac{7}{2}$��
����F��������$\frac{7}{2}$��0����
��CF=$\frac{7}{2}$-��-4��=$\frac{15}{2}$��
���BCF�����S=$\frac{1}{2}$��3CF=$\frac{1}{2}$��3��$\frac{15}{2}$=$\frac{45}{4}$��
��2����Ϻ���ͼ���֪��
��x��2ʱ��kx+b��mx+t����x��2ʱ��kx+b��mx+t����x=2ʱ��kx+b=mx+t��
�ʴ�Ϊ����2����2��=2��
��3�����H��������n��0����
�ߵ�O��0��0������B��2��3����
��OB=$\sqrt{��2-0��^{2}+��3-0��^{2}}$=$\sqrt{13}$��OH=|n|��BH=$\sqrt{��n-2��^{2}+��0-3��^{2}}$��
��OBH������������������
�ٵ�OB=OHʱ����$\sqrt{13}$=|n|����ã�n=��$\sqrt{13}$��
��ʱ��H������Ϊ��-$\sqrt{13}$��0����$\sqrt{13}$��0����
�ڵ�OB=BHʱ����$\sqrt{13}$=$\sqrt{��n-2��^{2}+��0-3��^{2}}$����ã�n=0����ȥ������n=4��
��ʱ��H������Ϊ��4��0����
�۵�OH=BHʱ����|n|=$\sqrt{��n-2��^{2}+��0-3��^{2}}$����ã�n=$\frac{13}{4}$��
��ʱ��H������Ϊ��$\frac{13}{4}$��0����
���Ͽ�֪����H������Ϊ��-$\sqrt{13}$��0������$\sqrt{13}$��0������4��0����$\frac{13}{4}$��0����
���� ���⿼����һ�κ�����Ӧ�á�����ϵ������������ʽ����Ϻ���ͼ��������ʽ�������ľ��빫ʽ�Լ����������ε����ʣ�����Ĺؼ��ǣ���1������ϵ������������ʽ����2����Ϻ���ͼ��ⲻ��ʽ����3���ֵ��������ε�����������ǣ����������е��⣬�ѶȲ���������͵���Ŀʱ�������������ҳ�����δ֪���ķ��̣����飩�ǹؼ���


 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
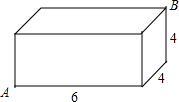 ��ͼ����һ��������ij��������߷ֱ��� 6��4��5���ڵ���A����һֻ���ϣ�����Ե�����������B����ʳ���Ҫ���е����·���Ƕ��٣�
��ͼ����һ��������ij��������߷ֱ��� 6��4��5���ڵ���A����һֻ���ϣ�����Ե�����������B����ʳ���Ҫ���е����·���Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10�� | B�� | 30�� | C�� | 40�� | D�� | 35�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
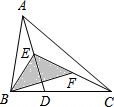 ��ͼ��D�ǡ�ABC�ı�BC������һ�㣬E��F�ֱ����߶�AD��CE���е㣬�ҡ�ABC�����Ϊ20cm2�����BEF�������
��ͼ��D�ǡ�ABC�ı�BC������һ�㣬E��F�ֱ����߶�AD��CE���е㣬�ҡ�ABC�����Ϊ20cm2�����BEF��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -16 | B�� | $\frac{1}{16}$ | C�� | 16 | D�� | $-\frac{1}{16}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com