
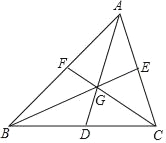
【题目】如图,点D、E、F分别为△ABC三边的中点,如果△ABC的面积为S,那么以AD、BE、CF为边的三角形的面积是_____.
【答案】![]()
【解析】分析:延长AD至G,使得DG=AD,连接BG,CG,取BG的中点H,连接CH,FH,依据三角形中线、中位线的性质以及平行四边形的性质,即可得到△CHG的面积=△BCG的面积的一半=平行四边形ABGC的面积的![]() =
=![]() S,△BFH的面积=△ABG的面积的
S,△BFH的面积=△ABG的面积的![]() =
=![]() S,△ACF的面积=
S,△ACF的面积=![]() S,进而得出△CFH的面积=2S﹣
S,进而得出△CFH的面积=2S﹣![]() S﹣
S﹣![]() S﹣
S﹣![]() S=
S=![]() S.
S.
详解:
如图所示,延长AD至G,使得DG=AD,连接BG,CG,则△ACD≌△GBD,△ABD≌△GCD,四边形ABGC为平行四边形,
∴四边形ABGC的面积=2S,
取BG的中点H,连接CH,FH,则BH∥CE,BH=CE,故四边形BHCE是平行四边形,
∴BE=CH,
由题可得,FH是△ABG的中位线,
∴FH=![]() AG=AD,
AG=AD,
∴△CFH即为以AD、BE、CF为边的三角形,
∵△CHG的面积=△BCG的面积的一半=平行四边形ABGC的面积的![]() =
=![]() S,
S,
△BFH的面积=△ABG的面积的![]() =
=![]() S,
S,
△ACF的面积=![]() S,
S,
∴△CFH的面积=2S﹣![]() S﹣
S﹣![]() S﹣
S﹣![]() S=
S=![]() S,
S,
故答案为:![]() S.
S.


科目:初中数学 来源: 题型:
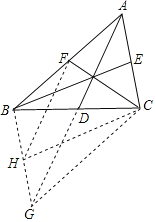
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
①﹣6﹣(+5)+23+|﹣![]() |
|
②计算:﹣12019+![]() ÷
÷![]() ﹣
﹣![]() ×(﹣9)
×(﹣9)
③计算:[-2﹣8×![]() ]÷(﹣2)3
]÷(﹣2)3
④课堂上老师出了一道计算题。
计算:![]() +
+![]() -(
-(![]() )-14+(
)-14+(![]() ),小明一看,太复杂了,怎么解呢?你能帮助小明解决这个问题吗?试试看。
),小明一看,太复杂了,怎么解呢?你能帮助小明解决这个问题吗?试试看。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设计调查问卷时,下列提问是否合适?如果不合适的话应该怎样改进?
(1)你上学时使用的交通工具是
![]() .汽车
.汽车![]() .摩托车
.摩托车![]() .步行
.步行![]() .其他
.其他
(2)你对老师的教学满意吗?
![]() .比较满意
.比较满意![]() .满意
.满意![]() .非常满意.
.非常满意.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,折线ABCDE描述了一汽车在某一直路上行驶时汽车离出发地的距离s(千米)和行驶时间t(小时)间的变量关系,则下列结论正确的是( )
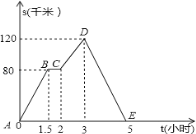
A. 汽车共行驶了120千米
B. 汽车在行驶途中停留了2小时
C. 汽车在整个行驶过程中的平均速度为每小时24千米
D. 汽车自出发后3小时至5小时间行驶的速度为每小时60千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学海书店购一批故事书进行销售,其进价为每本40元,如果按每本故事书50元进行出售,每月可以售出500本故事书,后来经过市场调查发现,若每本故事书涨价1元,则故事书的销量每月减少20本.
(1)若学海书店要保证每月销售此种故事书盈利6000元,同时又要使购书者得到实惠,则每本故事书需涨价多少元;
(2)若使该故事书的月销量不低于300本,则每本故事书的售价应不高于多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣x的图象与反比例函数y=![]() (x<0)的图象相交于点A(﹣4,m).
(x<0)的图象相交于点A(﹣4,m).
(1)求反比例函数y=![]() 的解析式;
的解析式;
(2)若点P在x轴上,AP=5,直接写出点P的坐标.
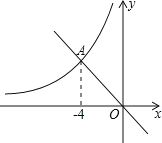
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
![]()
(1)当0<t<5时,用含t的式子填空:
BP=_______,AQ=_______;
(2)当t=2时,求PQ的值;
(3)当PQ=![]() AB时,求t的值.
AB时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com