
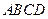 的对角线
的对角线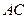 和
和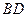 相交于点
相交于点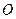 ,
,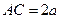 ,
,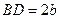 ,
,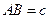
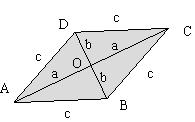
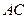 和
和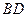 具有怎样的位置关系?
具有怎样的位置关系?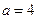 ,
,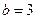 ,求
,求科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 究:
究:
 现:在一个四边形中,只要有一组对边平行,就可以剪拼成平行四边形.
现:在一个四边形中,只要有一组对边平行,就可以剪拼成平行四边形.

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.9英寸(23厘米) | B.21英寸(54厘米) | C.29英寸(74厘米) | D.34英寸(87厘米) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
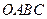 的顶点
的顶点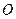 在坐标原点处,点
在坐标原点处,点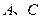 分别在
分别在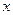 轴、
轴、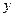 轴的正半轴上,点
轴的正半轴上,点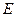 是
是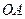 边上的点(不与点
边上的点(不与点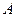 重合),
重合), ,且与正方形外角平分线
,且与正方形外角平分线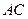 交于点
交于点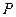 .
.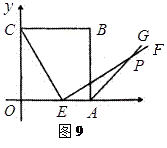
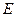 坐标为
坐标为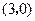 时,试证明
时,试证明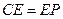 ;
;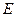 坐标为(3,0)”改为“点
坐标为(3,0)”改为“点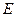 坐标为(
坐标为(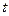 ,0)(
,0)(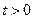 )”,结论
)”,结论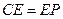 是否仍然成立,请说明理由;
是否仍然成立,请说明理由;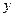 轴上是否存在点
轴上是否存在点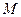 ,使得四边形
,使得四边形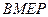 是平行四边形?若存在,用
是平行四边形?若存在,用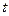 表示点
表示点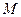
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com