
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 在
在![]() 上,且
上,且![]() 的半径为
的半径为![]() .问当
.问当![]() 在什么范围内取值时
在什么范围内取值时![]() 与
与![]() 相离、相切、相交?
相离、相切、相交?

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:
为解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可以将x2﹣1视为一个整体,然后设x2﹣1=y,则原方程化为y2﹣5y+4=0,解此方程得:y1=1,y2=4.
当y=1时,x2﹣1═1,∴x=±![]() .
.
当y=4时,x2﹣1═4,∴x=±![]() .
.
∴原方程的解为:x1=![]() ,x2=﹣
,x2=﹣![]() ,x3=
,x3=![]() ,x4=﹣
,x4=﹣![]() .
.
以上方法叫做换元法解方程,达到了降次的目的,体现了转化思想.
运用上述方法解方程:x4﹣8x2+12=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=![]() ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB.

(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() ,
,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点.如果点
的中点.如果点![]() 在线段
在线段![]() 上以每秒2厘米的速度由
上以每秒2厘米的速度由![]() 点向
点向![]() 点运动,同时,点
点运动,同时,点![]() 在线段
在线段![]() 上以每秒
上以每秒![]() 厘米的速度由
厘米的速度由![]() 点向
点向![]() 点运动,设运动时间为
点运动,设运动时间为![]() (秒)
(秒)![]() .
.

(1)用含![]() 的代数式表示
的代数式表示![]() 的长度;
的长度;
(2)若点![]() 、
、![]() 的运动速度相等,经过1秒后,
的运动速度相等,经过1秒后,![]() 与
与![]() 是否全等,请说明理由;
是否全等,请说明理由;
(3)若点![]() 、
、![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度
的运动速度![]() 为多少时,能够使
为多少时,能够使![]() 与
与![]() 全等?
全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,高速公路上有A、B两点相距25km,C、D为两村庄,已知DA=10km,CB=15km.DA⊥AB于A,CB⊥AB于B,现要在AB上建一个服务站E,使得C、D两村庄到E站的距离相等,则AE的长是( )km.

A.5B.10C.15D.25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),Rt△ABC中,∠ACB=-90°,CD⊥AB,垂足为D.AF平分∠CAB,交CD于点E,交CB于点F
(1)求证:CE=CF.
(2)将图(1)中的△ADE沿AB向右平移到△A’D’E’的位置,使点E’落在BC边上,其它条件不变,如图(2)所示.试猜想:BE'与CF有怎样的数量关系?请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
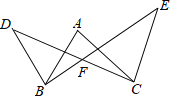
【题目】如图,AB=BD,AC=CE,DC、BE交于点F,∠ABD=∠ACE=60°.
(1)求证:BE=CD;
(2)求∠A+∠ABF+∠ACF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com