
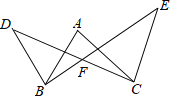
【题目】如图,AB=BD,AC=CE,DC、BE交于点F,∠ABD=∠ACE=60°.
(1)求证:BE=CD;
(2)求∠A+∠ABF+∠ACF的值.
【答案】(1)见解析;(2)∠ABF+∠ACF+∠BAC=120°.
【解析】
(1)先证△ABD,△ACE是等边三角形,由“SAS”可证△ADC≌△ABE,可得BE=CD;
(2)由全等三角形的性质可得∠ABF=∠ADC,由三角形内角和定理可求解.
证明:(1)如图,连接AD,AE,
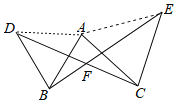
∵AB=BD,AC=CE,∠ABD=∠ACE=60°.
∴△ABD,△ACE是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠EAC,
∴∠DAC=∠BAE,且AD=AB,AC=AE,
∴△ADC≌△ABE(SAS)
∴BE=CD;
(2)∵△ADC≌△ABE,
∴∠ABF=∠ADC,
∵∠ADC+∠ACF+∠DAB+∠BAC=180°,
∴∠ABF+∠ACF+∠BAC=120°


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
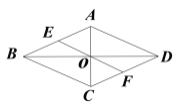
【题目】如图,在菱形ABCD中,AC和BD相交于点O,过点O的线段EF与一组对边AB,CD分别相交于点E,F.
(1)求证:AE=CF;
(2)若AB=2,点E是AB中点,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB<AC,M是BC边的中点,MN⊥BC交AC于点N,动点P在线段BA上以每秒![]() cm的速度由点B向点A运动.同时,动点Q在线段AC上由点N向点C运动,且始终保持MQ⊥MP.一个点到终点时两个点同时停止运动,设运动的时间为t秒(t>0).
cm的速度由点B向点A运动.同时,动点Q在线段AC上由点N向点C运动,且始终保持MQ⊥MP.一个点到终点时两个点同时停止运动,设运动的时间为t秒(t>0).
(1)求证:△PBM∽△QNM.
(2)若∠ABC=60°,AB=4![]() cm,
cm,
①求动点Q的运动速度;
②设△APQ的面积为S(cm2),求S与t的等量关系式(不必写出t的取值范围).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证:△ABP∽△BCP;
②若PA=3,PC=4,则PB= .
(2)已知锐角△ABC,分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD 相交于P点.如图(2)
①求∠CPD的度数;
②求证:P点为△ABC的费马点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知函数![]() 为反比例函数.
为反比例函数.
己知函数![]() 为反比例函数.
为反比例函数.
![]() 求
求![]() 的值;
的值;
![]() 它的图象在第________象限内,在各象限内,
它的图象在第________象限内,在各象限内,![]() 随
随![]() 增大而________;(填变化情况)
增大而________;(填变化情况)
![]() 当
当![]() 时,此函数的最大值为________,最小值为________.
时,此函数的最大值为________,最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com