Question

【题目】如图(1)，Rt△ABC中，∠ACB=-90°，CD⊥AB，垂足为D．AF平分∠CAB，交CD于点E，交CB于点F

（1）求证：CE=CF．

（2）将图（1）中的△ADE沿AB向右平移到△A’D’E’的位置，使点E’落在BC边上，其它条件不变，如图（2）所示．试猜想：BE'与CF有怎样的数量关系?请证明你的结论．

Answer 1

【答案】（1）见解析

（2）相等。证明见解析

【解析】

（1）根据平分线的定义可知∠CAF=∠EAD，再根据已知条件以及等量代换即可证明CE=CF，

（2）根据题意作辅助线过点E作EG⊥AC于G，根据平移的性质得出D′E′=DE，再根据已知条件判断出△CEG≌△BE′D′，可知CE=BE′，再根据等量代换可知BE′=CF．

（1）证明：∵AF平分∠CAB，

∴∠CAF=∠EAD，

∵∠ACB=90°，

∴∠CAF+∠CFA=90°，

∵CD⊥AB于D，

∴∠EAD+∠AED=90°，

∴∠CFA=∠AED，又∠AED=∠CEF，

∴∠CFA=∠CEF，

∴CE=CF；

（2）猜想：BE′=CF．

证明：如图，

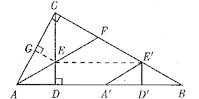
过点E作EG⊥AC于G，连接EE′，

又∵AF平分∠CAB，ED⊥AB，EG⊥AC，

∴ED=EG，

由平移的性质可知：D′E′=DE，

∴D′E′=GE，

∵∠ACB=90°，

∴∠ACD+∠DCB=90°

∵CD⊥AB于D，

∴∠B+∠DCB=90°，

∴∠ACD=∠B，

在△CEG与△BE′D′中，

，

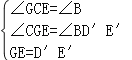∴△CEG≌△BE′D′（AAS），

∴CE=BE′，

由（1）可知CE=CF，

∴BE′=CF．