
【题目】如图,点C为线段AB上一点,分别以AB、AC、CB为底作顶角为120°的等腰三角形,顶角顶点分别为D、E、F(点E、F在AB的同侧,点D在另一侧)
(1)如图1,若点C是AB的中点,则∠AED= ;
(2)如图2,若点C不是AB的中点
①求证:△DEF为等边三角形;
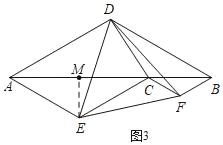
②连接CD,若∠ADC=90°,AB=3,请直接写出EF的长.

【答案】(1) 90°;(2)①见解析;②![]()
【解析】
(1)如图1,过E作EH⊥AB于H,连接CD,设EH=x,则AE=2x,AH=![]() x,根据等腰三角形的性质得到∠DAC=30°,进而得到DC=CE,又因为EH∥DC,∴∠HED=∠EDC=∠CED,再进一步得到∠AEH=60°,∠HED=30°,即可求出∠AED的大小;(2)①延长FC交AD于H,连接HE,如图2,根据等腰三角形的性质得到∠FCB=∠FBC=30°,∠DAB=∠DBA=30°,∠EAC=∠ECA=30°,进而得到AD∥EC∥BF,AE∥CF∥BD,所以四边形BDHF、四边形AECH是平行四边形,进而得到△AEH是等边三角形,再根据SAS判定定理得到△DHE≌△FCE,∴∠DEF=∠CEH=60°,∴△DEF是等边三角形;②如图3,过E作EM⊥AB于M,根据等腰三角形的性质,求出CD、CE的长,再根据勾股定理求出DE的长,因为△DEF是等边三角形,∴EF=DE,即可得解.
x,根据等腰三角形的性质得到∠DAC=30°,进而得到DC=CE,又因为EH∥DC,∴∠HED=∠EDC=∠CED,再进一步得到∠AEH=60°,∠HED=30°,即可求出∠AED的大小;(2)①延长FC交AD于H,连接HE,如图2,根据等腰三角形的性质得到∠FCB=∠FBC=30°,∠DAB=∠DBA=30°,∠EAC=∠ECA=30°,进而得到AD∥EC∥BF,AE∥CF∥BD,所以四边形BDHF、四边形AECH是平行四边形,进而得到△AEH是等边三角形,再根据SAS判定定理得到△DHE≌△FCE,∴∠DEF=∠CEH=60°,∴△DEF是等边三角形;②如图3,过E作EM⊥AB于M,根据等腰三角形的性质,求出CD、CE的长,再根据勾股定理求出DE的长,因为△DEF是等边三角形,∴EF=DE,即可得解.
(1)如图1,过E作EH⊥AB于H,连接CD,
设EH=x,则AE=2x,AH=![]() x,
x,
∵AE=EC,
∴AC=2AH=2![]() x,
x,
∵C是AB的中点,AD=BD,
∴CD⊥AB,
∵∠ADB=120°,
∴∠DAC=30°,
∴DC=2x,
∴DC=CE=2x,
∵EH∥DC,
∴∠HED=∠EDC=∠CED,
∵∠AEH=60°,∠AEC=120°,
∴∠HEC=60°,
∴∠HED=30°,
∴∠AED=∠AEH+∠HED=90°;
故答案为:90°;
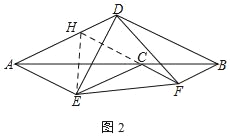
(2)①延长FC交AD于H,连接HE,如图2,
∵CF=FB,
∴∠FCB=∠FBC,
∵∠CFB=120°,
∴∠FCB=∠FBC=30°,
同理:∠DAB=∠DBA=30°,∠EAC=∠ECA=30°,
∴∠DAB=∠ECA=∠FBD,
∴AD∥EC∥BF,
同理AE∥CF∥BD,
∴四边形BDHF、四边形AECH是平行四边形,
∴EC=AH,BF=HD,
∵AE=EC,
∴AE=AH,
∵∠HAE=60°,
∴△AEH是等边三角形,
∴AE=AH=HE=CE,∠AHE=∠AEH=60°,
∴∠DHE=120°,
∴∠DHE=∠FCE.
∵DH=BF=FC,
∴△DHE≌△FCE(SAS),
∴DE=EF,∠DEH=∠FEC,
∴∠DEF=∠CEH=60°,
∴△DEF是等边三角形;
②如图3,过E作EM⊥AB于M,
∵∠ADC=90°,∠DAC=30°,
∴∠ACD=60°,
∵∠DBA=30°,
∴∠CDB=∠DBC=30°,
∴CD=BC=![]() AC,
AC,
∵AB=3,
∵AC=2,BC=CD=1,
∵∠ACE=30°,∠ACD=60°,
∴∠ECD=30°+60°=90°,
∵AE=CE,
∴CM=![]() AC=1,
AC=1,
∵∠ACE=30°,
∴CE=![]() ,
,
Rt△DEC中,DE=![]() =
=![]() =
=![]() ,
,
由①知:△DEF是等边三角形,
∴EF=DE=![]() .
.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
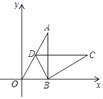
【题目】如图,直线![]() 经过点A,作AB⊥x轴于点B,将△ABO绕点B顺时针旋转60°得到△CBD,若点B的坐标为(1,0),则点C的坐标为( )
经过点A,作AB⊥x轴于点B,将△ABO绕点B顺时针旋转60°得到△CBD,若点B的坐标为(1,0),则点C的坐标为( )
A.(3,![]() )B.(
)B.(![]() ,
,![]() )C.(3,
)C.(3,![]() )D.(
)D.(![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于![]() 的一元二次方程
的一元二次方程![]() 有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,正确的是( )
有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,正确的是( )
①方程![]() 是倍根方程;②若
是倍根方程;②若![]() 是倍根方程,则
是倍根方程,则![]() 或
或![]() ③若点
③若点![]() 在双曲线
在双曲线![]() 的图像上,则关于
的图像上,则关于![]() 的方程
的方程![]() 是倍根方程;
是倍根方程;
A. ①B. ①②C. ①③D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
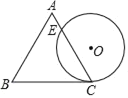
【题目】如图是某商品标牌的示意图,⊙O与等边△ABC的边BC相切于点C,且⊙O的直径与△ABC的高相等,已知等边△ABC边长为4,设⊙O与AC相交于点E,则AE的长为( )
A.![]() B.1C.
B.1C.![]() ﹣1D.
﹣1D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O→C→B→A运动,点P的运动时间为t秒.则当t=____秒时,△ODP是腰长为5的等腰三角形?
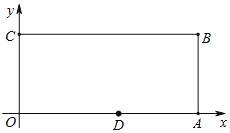
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①4a+2b+c>0;②abc<0;③b<a﹣c;④3b>2c;⑤a+b<m(am+b),(m≠1的实数);其中正确结论的个数为( )
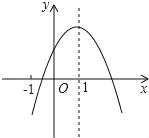
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,⊙O的半径为4,点A是⊙O上一点,直线l过点A;P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l于点B,交⊙O于点E,直径PD延长线交直线l于点F,点A是![]() 的中点.
的中点.
(1)求证:直线l是⊙O的切线;
(2)若PA=6,求PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
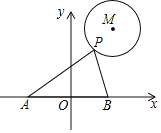
A. 3B. 4C. 6D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com