解:(1)在⊙O
1中,∠C和∠ABE所对的都是弧AE
∴∠C=∠B
同理可在⊙O
2中得出:∠D=∠B,
∴∠C=∠D
∴CE∥DF
(2)由(1)知:∠C=∠D,
在△CEG和△DFG中

∴△CEG≌△DFG(ASA)
∴CE=DF.
分析:(1)可根据圆周角定理来解.要证CE∥DF,关键是证明∠C=∠D,以∠ABE为中间值,根据所求的两个角与∠ABE在不同的圆中对应的圆弧相等来得出所求角相等,从而得出CE∥DF.
(2)可通过证明三角形CEG和FGD全等来得出结论,这两个三角形中已知的条件有:CG=GD,一组对顶角,只要再证得一组对应角相等即可得出两三角形全等,由(1)的平行线可知:∠C=∠D,这样就构成了两三角形全等的所有条件,便可得出CE=DF.
点评:本题主要考查了全等三角形的判定和圆周角定理,通过圆周角得出三角形全等是本题解题的关键.

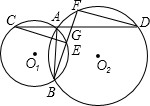 ,连接DF、CE.
,连接DF、CE.

