
【题目】如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以点D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN.
(1)求证:MN=BM+NC;
(2)求△AMN的周长.

【答案】(1)证明见解析;(2)6.
【解析】
(1)先证明△BDF≌△CDN,得出∠BDF=∠CDN,DF=DN,同时再证明△DMN≌△DMF,得出MN=MF=MB+BF=MB+CN.
(2)根据MN=MB+CN,得出△AMN的周长为AM+AN+MN=AM+MB+AN+CN=AB+AC=6.
解:(1)∵△BDC是等腰三角形,且∠BDC=120°,∴∠BCD=∠DBC=30°.
∵△ABC是等边三角形,∴∠ABC=∠BCA=60°,
∴∠DBA=∠DCA=90°,
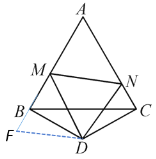
延长AB至F,使BF=CN,连接DF,
由SAS可证△BDF≌△CDN,
∴∠BDF=∠CDN,DF=DN,
∵∠MDN=60°,∴∠FDM=∠BDM+∠CDN=60°,
由SAS可证△DMN≌△DMF,
∴MN=MF=MB+BF=MB+CN
(2)由(1)知MN=MB+CN,
∴△AMN的周长为AM+AN+MN=AM+MB+AN+CN=AB+AC=6


科目:初中数学 来源: 题型:
【题目】(1)在图中作出△ABC关于直线m对称的△A′B′C′,并写出A′、B′、C′三点的坐标(2)猜想:坐标平面内任意点P(x,y)关于直线m对称点P′的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若点M是y轴正半轴上任意一点,过点M作PQ∥x轴,分别交函数y=![]() (x<0)和y=
(x<0)和y=![]() (x>0)的图象于点P和Q,连接OP和OQ.以下列结论:
(x>0)的图象于点P和Q,连接OP和OQ.以下列结论:
①∠POQ不可能等于90°;
②![]() ;
;
③这两个函数的图象一定关于y轴对称;
④若S△POM=S△QOM,则k1+k2=0;
⑤△POQ的面积是![]() (|k1|+|k2|).
(|k1|+|k2|).
其中正确的有_____(填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某校招聘教师一名,现有甲、乙、丙三人通过专业知识、讲课、答辩三项测试,他们各自的成绩如下表所示:
应聘者 | 专业知识 | 讲课 | 答辩 |
甲 | 70 | 85 | 80 |
乙 | 90 | 85 | 75 |
丙 | 80 | 90 | 85 |
按照招聘简章要求,对专业知识、讲课、答辩三项赋权5:4:1.请计算三名应聘者的平均成绩,从成绩看,应该录取谁?
(2)我市举行了某学科实验操作考试,有A、B、C、D四个实验,规定每位学生只参加其中一个实验的考试,并由学生自己抽签决定具体的考试实验.小王,小张,小厉都参加了本次考试.
①小厉参加实验D考试的概率是 ;
②用列表或画树状图的方法求小王、小张抽到同一个实验的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,点M,N同时从点B出发,分别在BC,BA上运动,若点M的运动速度是每秒2个单位长度,且是点N运动速度的2倍,当其中一个点到达终点时,停止一切运动.以MN为对称轴作△MNB的对称图形△MNB1.点B1恰好在AD上的时间为______秒.在整个运动过程中,△MNB1与矩形ABCD重叠部分面积的最大值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC.
(1)求证:△BDA≌△CEA;
(2)请判断△ADE是什么三角形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y = kx + b的图象经过点(1,-2)和(2,0).
(1)求这个一次函数的关系式:
(2)将该函数的图象沿x轴向左平移3个单位后,求所得图象对应的函数表达式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com