
【题目】已知:如图,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH. 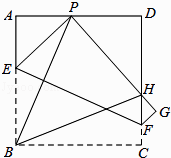
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论.
【答案】
(1)证明:∵PE=BE,
∴∠EBP=∠EPB.
又∵∠EPH=∠EBC=90°,
∴∠EPH﹣∠EPB=∠EBC﹣∠EBP.
即∠PBC=∠BPH.
又∵AD//BC,
∴∠APB=∠PBC.
∴∠APB=∠BPH
(2)解:△PHD的周长不变为定值8.
证明:过B作BQ⊥PH,垂足为Q.
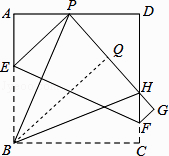
由(1)知∠APB=∠BPH,
在△ABP和△QBP中,
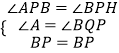 ,
,
∴△ABP≌△QBP(AAS).
∴AP=QP,AB=QB.
又∵AB=BC,
∴BC=BQ.
又∵∠C=∠BQH=90°,BH=BH,
∴Rt△BCH≌Rt△BQH(HL).
∴CH=QH.
∴△PHD的周长为:PD+DH+PH=AP+PD+DH+HC=AD+CD=8
【解析】(1)根据翻折变换的性质得出∠PBC=∠BPH,进而利用平行线的性质得出∠APB=∠PBC即可得出答案;(2)首先证明△ABP≌△QBP,进而得出△BCH≌△BQH,即可得出PD+DH+PH=AP+PD+DH+HC=AD+CD=8;
【考点精析】关于本题考查的正方形的性质和翻折变换(折叠问题),需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;② ![]() ;③△PMN为等边三角形;④当∠ABC=45°时,BN=
;③△PMN为等边三角形;④当∠ABC=45°时,BN= ![]() PC.其中正确的个数是( )
PC.其中正确的个数是( ) 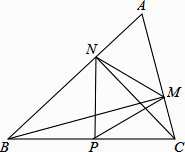
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A,B,C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒4个单位长度的速度向终点C移动,设移动时间为t秒.
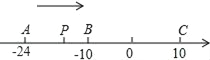
(1)用含t的代数式表示点P与A的距离:PA= ;点P对应的数是 ;
(2)动点Q从点B出发,以每秒1个单位长度的速度向终点C移动,若P、Q同时出发,求:当点P运动多少秒时,点P和点Q间的距离为8个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】植树节来临之际,学校准备购进一批树苗,已知2棵甲种树苗和5棵乙种树苗共需113元;3棵甲种树苗和2棵乙种树苗共需87元.
(1)求一棵甲种树苗和一棵乙种树苗的售价各是多少元?
(2)学校准备购进这两种树苗共100棵,并且乙种树苗的数量不多于甲种树苗数量的2倍,请设计出最省钱的购买方案,并求出此时的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
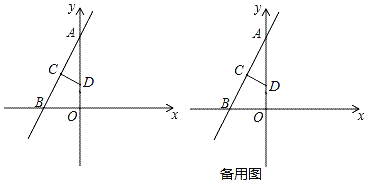
【题目】如图,在平面直角坐标系中,A(0,8),B(﹣4,0),线段AB的垂直平分线CD分别交AB、OA于点C、D,其中点D的坐标为(0,3).
(1)求直线AB的解析式;
(2)求线段CD的长;
(3)点E为y轴上一个动点,当△CDE为等腰三角形时,求E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为贯彻党的“绿水青山就是金山银山”的理念,我市计划购买甲、乙两种树苗共7000株用于城市绿化,甲种树苗每株24元,一种树苗每株30元![]() 相关资料表明:甲、乙两种树苗的成活率分别为
相关资料表明:甲、乙两种树苗的成活率分别为![]() 、
、![]() .
.
![]() 若购买这两种树苗共用去180000元,则甲、乙两种树苗各购买多少株?
若购买这两种树苗共用去180000元,则甲、乙两种树苗各购买多少株?
![]() 若要使这批树苗的总成活率不低于
若要使这批树苗的总成活率不低于![]() ,则甲种树苗至多购买多少株?
,则甲种树苗至多购买多少株?
![]() 在
在![]() 的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.
的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )

A. 13s B. 8s C. 6s D. 5s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= ![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y= ![]() 的图象上,则k的值为 .
的图象上,则k的值为 . 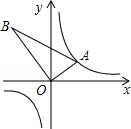
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com