
【题目】在![]() 中,
中,![]() ,分别以
,分别以![]() 、
、![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() .
.
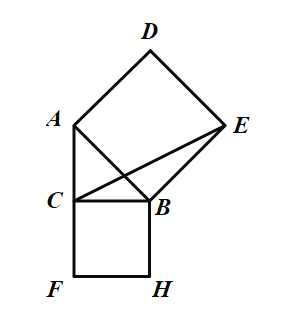

(1)当![]() 时,正方形
时,正方形![]() 的周长
的周长![]() ________(用含
________(用含![]() 的代数式表示);
的代数式表示);
(2)连接![]() .试说明:三角形
.试说明:三角形![]() 的面积等于正方形
的面积等于正方形![]() 面积的一半.
面积的一半.
(3)已知![]() ,且点
,且点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 是线段
是线段![]() 上的动点,当
上的动点,当![]() 点和
点和![]() 点在移动过程中,
点在移动过程中,![]() 的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
【答案】(1)4![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() 的周长最小值为
的周长最小值为![]()
【解析】
(1)根据正方形的周长公式即可得解;
(2)首先判定![]() ,然后即可判定
,然后即可判定![]() ,即可得解;
,即可得解;
(3)利用对称性,当A′、P、Q、F共线时![]() 的周长取得最小值,然后利用勾股定理即可得解.
的周长取得最小值,然后利用勾股定理即可得解.
(1)由题意,得正方形![]() 的周长为
的周长为![]() ;
;
(2)连接![]() ,如图所示:
,如图所示:
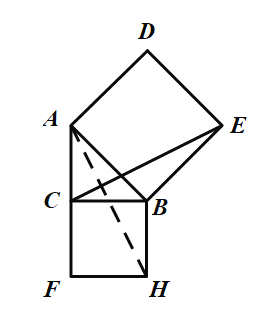
∵∠CBH=∠ABE=90°
∴∠CBH+∠ABC=∠ABE+∠ABC
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
∴![]() 的面积
的面积![]() 的面积
的面积![]() 正方形
正方形![]() 的面积
的面积
(3)作点![]() 关于
关于![]() 的对称点
的对称点![]() ,∴
,∴![]()
点![]() 关于
关于![]() 的对称点
的对称点![]() ,∴
,∴![]()
∵![]() 的周长为
的周长为![]() ,即为
,即为![]()
当A′、P、Q、F共线时![]() 的周长取得最小值,
的周长取得最小值,
∴![]() 的周长的最小值为
的周长的最小值为![]()
过![]() 作
作![]() 的延长线于
的延长线于![]() ,
,
∵![]()
∴∠CAB=45°,AB=AD=![]()
∵∠DAB=90°
∴∠MAA′=45°
∴![]() 为等腰直角三角形
为等腰直角三角形
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴![]() 的周长最小值为
的周长最小值为![]() .
.



科目:初中数学 来源: 题型:
【题目】一列高铁列车从甲地匀速驶往乙地,一列特快列车从乙地匀速驶往甲地,两车同时出发,设特快列车行驶的时间为x(单位:时),特快列车与高铁列车之间的距离为y(单位:千米),y与x之间的函数关系如图所示,则图中线段CD所表示的y与x之间的函数关系式是_____.
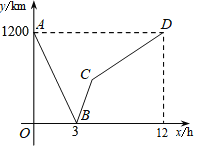
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知![]() ,
,![]() 是平面上的任意一点,过点
是平面上的任意一点,过点![]() 作
作![]() ,
,![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() ,求
,求![]() 的度数.
的度数.
(2)探究![]() 与
与![]() 有什么关系?(直接写出结论)
有什么关系?(直接写出结论)
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在BC,CD上, ΔAEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE,其中结论正确的个数为( )
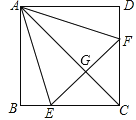
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
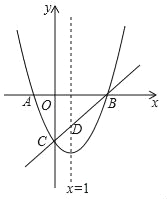
【题目】如图,已知抛物线y=x2+bx+c与x轴交于A、B(点A在点B的左侧),与y轴交于点C(0,﹣3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
(1)求抛物线的函数解析式;
(2)求直线BC的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
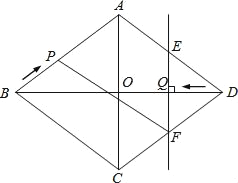
【题目】如图,在菱形ABCD中,AC,BD交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为lcm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为lcm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q.F,当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
(1)求菱形ABCD的面积;
(2)当t=1时,求QF长;
(3)是否存在某一时刻t,使四边形APFD是平行四边形?若存在,求出t值,若不存在,请说明理由;
(4)设△DEF的面积为s(cm2),试用含t的代数式表示S,并求t为何值时,△DEF的面积与△BPC的面积相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
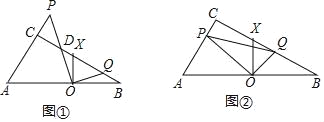
【题目】(1)如图①所示,∠ACB=∠POQ=∠XOB=90°.
①求证:∠POA=∠XOQ;
②判断△PAO和△QXO是否相似,如两个三角形相似请给出证明,如不相似,说明理由;
(2)如图②.在△ABC中,∠ACB=90°,∠CBA=30°,AO=BO,点P在AC上,点Q在BC上,且∠POQ=90°,XO⊥AB交BC于X,AC=4cm,AP=x(0<x<4),设△PCQ的面积为y,求y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
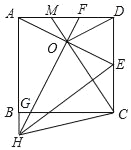
【题目】如图,正方形ABCD中,E为CD的中点,AE的垂直平分线分别交AD,BC及AB的延长线于点F,G,H,连接HE,HC,OD,连接CO并延长交AD于点M.则下列结论中:
①FG=2AO;②OD∥HE;③![]() ;④2OE2=AHDE;⑤GO+BH=HC
;④2OE2=AHDE;⑤GO+BH=HC
正确结论的个数有( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港珠澳大桥是世界最长的跨海大桥,连接香港大屿山、澳门半岛和广东省珠海市,其中珠海站到香港站全长约55千米,2018年10月24日上午9时正式通车.一辆观光巴士自珠海站出发,25分钟后,一辆小汽车从同一地点出发,结果同时到达香港站.已知小汽车的速度是观光巴士的1.6倍,求观光巴士的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com