练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

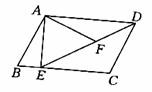
    如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E,连接DE,F为线段CD上一点,且∠AFE=∠B。

    （1）求证△ADF∽△DEC；

    （2）若AB=4,AD=3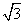,AE=3,求AF的长.


    （1）∵四边形ABCD 是平行四边形∴∠ADF=∠CED，∠C＋∠B=180°。

           又∠AFD＋∠AFE=180°，∠AFE=∠B，

          ∴∠AFD=∠C，∴△ADF∽△DEC。

    （2）∵AB=4,AD=3,AE=3, AE⊥BC，∴AE⊥AD，CD=AB=4。

        在Rt△ADE中，由勾股定理得：DE=6

    由△ADF∽△DEC，得，即，解得：AF=2


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


     如果∠A=30°，则∠A的余角是　　　度；如果∠1+∠2=90°，∠1+∠3=90°，那么∠2与∠3的大小关系是　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


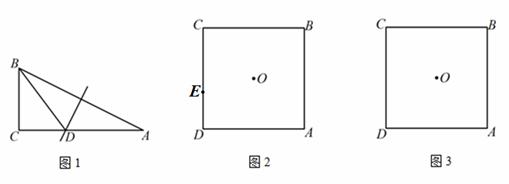
    （1）如图1，△ABC中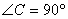，，AB的垂直平分线交AC于点D，连接BD.若AC=2，

            BC=1，则△BCD的周长为              ；   

    （2）O为正方形ABCD的中心，E为CD边上一点，F为AD边上一点，且△EDF的周长

    等于AD的长.

    ①在图2中求作△EDF（要求：尺规作图，不写作法，保留作图痕迹）；

    ②在图3中补全图形，求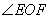的度数；

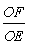    ③若，则的值为            . 

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    正比例函数y1＝kx的图象与反比例函数y2＝的图象的一个交点的坐标为(-1，-2)，则另一个交点的坐标是      .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    关于x的一元二次方程kx2+2x－1=0有两个不相等的实数根, 则k的取值范围是  (    )

    A. k>－1      B. k>1         C. k≠0                         D. k>－1且k≠0

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若(a－b):(a+b)=3:7, 则a:b=     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    把两块全等的直角三角形ABC和DEF叠放在一起，使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合，其中∠ABC=∠DEF=90°，∠C=∠F=45°，AB=DE=4，把三角板ABC固定不动，让三角板DEF绕点D旋转，设射线DE与射线AB相交于点P，射线DF与线段BC相交于点Q．

    （1）如图（1），当射线DF经过点B，即点Q与点B重合时，易证△APD∽△CDQ．此时，AP·CQ=        ．

    （2）将三角板DEF由图（1）所示的位置绕点O沿逆时针方向旋转，设旋转角为α．其中0°＜α＜90°，问AP·CQ的值是否改变？说明你的理由．

    （3）在（2）的条件下，设CQ=x，两块三角板重叠面积为y，求y与x的函数关系式．（图（2），图（3）供解题用）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    去括号：2a﹣（b+c）=　　　　　　．

    查看答案和解析>>

    同步练习册答案