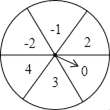
【题目】如图是一个平均被分成6等分的圆，每一个扇形中都标有相应的数字，甲乙两人分别转动转盘，设甲转动转盘后指针所指区域内的数字为x，乙转动转盘后指针所指区域内的数字为y（当指针在边界上时，重转一次，直到指向一个区域为止）．
（1）直接写出甲转动转盘后所指区域内的数字为负数的概率；
（2）用树状图或列表法，求出点（x，y）落在第二象限内的概率．
【答案】（1）甲转动转盘后所指区域内的数字为负数的概率为
；
（2）点（x，y）落在第二象限内的概率为
．
【解析】试题分析：(1)根据古典概率的知识,利用概率公式即可求得答案;
(2)根据题意列出表格,然后根据表格即可求得所有等可能的结果与点（x,y）落在第二象限内的情况,然后利用概率公式求解即可求得答案.
解：（1）∵一共有6种等可能的结果，甲转动转盘后所指区域内的数字为负数的有：﹣1，﹣2共2种情况，
∴甲转动转盘后所指区域内的数字为负数的概率为：
=
；
（2）根据题意，列表得：
甲 乙 | ﹣1 | ﹣2 | 0 | 2 | 3 | 4 |
﹣1 | （﹣1，﹣1） | （﹣2，﹣1） | （0，﹣1） | （2，﹣1） | （3，﹣1） | （4，﹣1） |
﹣2 | （﹣1，﹣2） | （﹣2，﹣2） | （0，﹣2） | （2，﹣2） | （3，﹣2） | （4，﹣2） |
0 | （﹣1，0） | （﹣2，0） | （0，0） | （2，0） | （3，0） | （4，0） |
2 | （﹣1，2） | （﹣2，2） | （0，2） | （2，2） | （3，2） | （4，2） |
3 | （﹣1，3） | （﹣2，3） | （0，3） | （2，3） | （3，3） | （4，3） |
4 | （﹣1，4） | （﹣2，4） | （0，4） | （2，4） | （3，4） | （4，4） |
∴点（x，y）的坐标一共有36种等可能的结果，且每种结果发生的可能性相等，其中点（x，y）落在第二象限的结果共有6种，
∴点（x，y）落在第二象限内的概率为：
=
．
阅读快车系列答案科目：初中数学 来源： 题型：
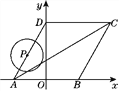
【题目】如图，菱形ABCD的顶点A，B在x轴上，点A在点B的左侧，点D在y轴的正半轴上，∠BAD＝60°，点A的坐标为(－2，0)．
(1)求线段AD所在直线的表达式；
(2)动点P从点A出发，以每秒1个单位长度的速度，按照A→D→C→B→A的顺序在菱形的边上匀速运动一周，设运动时间为t秒．求t为何值时，以点P为圆心、以1为半径的圆与对角线AC相切？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点A（3，4），点B为直线x=1上的动点，设B（－1，y）．
（1）如图①，若△ABO是等腰三角形且AO=AB时，求点B的坐标；
（2）如图②，若点C（x，0）且－1＜x＜3，BC⊥AC垂足为点C；
①当x=0时，求tan∠BAC的值；
②若AB与y轴正半轴的所夹锐角为α，当点C在什么位置时tanα的值最大？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了解本校七年级学生的数学作业完成情况，将完成情况分为四个等级：
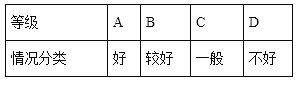
随机对该年级若干名学生进行了调查，然后把调查结果绘制成两幅不完整的统计图．请根据图中的信息解答下列问题：
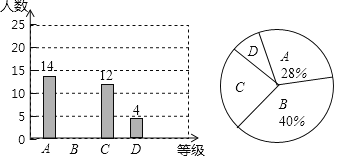
（1）共调查了多少名同学？补全条形统计图；
（2）完成等级为C等的对应扇形的圆心角的度数是 ；
（3）该年级共有700人，估计该年级数学作业完成等级为D等的人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，图1是AD∥BC的一张纸条，按图1→图2→图3，把这一纸条先沿EF折叠并压平，再沿BF折叠并压平，若图3中∠CFE=18°，则图2中∠AEF的度数为（ ）
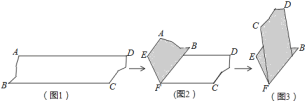
A.120°B.108°C.126°D.114°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面的材料并填空：
①(1﹣
)(1+)＝1﹣
，反过来，得1﹣＝(1﹣)(1+)＝×
；
②(1﹣
)(1+)＝1﹣
，反过来，得1﹣＝(1﹣)(1+)＝ × ；
③(1﹣
)(1+)＝1﹣
，反过来，得1﹣＝ ＝
；
利用上面的材料中的方法和结论计算下题：
(1﹣)(1﹣)(1﹣)……(1﹣
)(1﹣
)(1﹣
).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC=8，BC=12，点D从B出发以每秒2个单位的速度在线段BC上从过点B向点C运动，点E同时从点C出发，以每秒2个单位的速度在线段AC上从点A运动，连接AD、DE，设D、E两点运动时间为
秒.
(1)运动_____秒时，CD=3AE.
(2)运动多少秒时，△ABD≌△DCE能成立，并说明理由；
(3)若△ABD≌△DCE，∠BAC=
则∠ADE=_______(用含
的式子表示)。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，AC∥DF，直线AF分别直线BD、CE 相交于点G、H，∠1=∠2，求证：∠C=∠D．
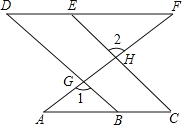
解：∵∠1=∠2（已知）
∠1=∠DGH（_________________）
∴∠2=__________（______________）
∴BD∥CE（________________）
∴∠C= ________（_______________）
又∵AC∥DF
∴∠D=∠ABG（________________）
∴∠C=∠D（________________）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明同学为调查某小学六个年级学生每周的零花钱情况，他在学校中随机抽取了400名学生进行调查统计并制成如下图表，
|
|
请根据图表提供的信息解答下列问题：
（1）a =__________，b =__________；
（2）补全频数分布直方图；
（3）若全校共有3000名学生，请你估计该校每周零花钱超过50元的学生有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
