
【题目】在平面直角坐标系中,已知![]() ,
,![]() ,
,![]()
![]() 且
且![]() ,
,![]() 的面积为3.
的面积为3.
(1)直接写出![]() ,
,![]() ,
,![]() .
.
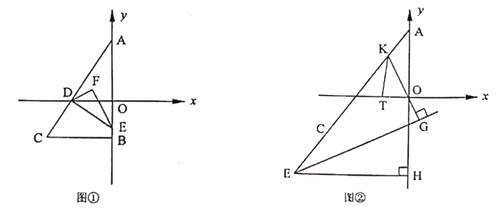
(2)如图①,设![]() 交
交![]() 轴于
轴于![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 、
、![]() 的角平分线交于点
的角平分线交于点![]() ,求
,求![]() 的大小.
的大小.
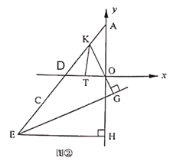
(3)如图②,点![]() 是
是![]() 延长线上动点,
延长线上动点,![]() 轴于点
轴于点![]() ,
,![]() 平分
平分![]() ,直线
,直线![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,
,![]() 平分
平分![]() 交
交![]() 轴于
轴于![]() 点,求
点,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的值是
的值是![]() .
.
【解析】
(1)根据算术平方根和绝对值的非负性求出a、b的值,再利用三角形的面积公式求出m的值即可;
(2)首先证明∠ADO=∠AED,根据三角形的内角和定理和角平分线的定义,即可解决问题;
(3)如图②中,先根据三角形外角的性质得:∠KTO=∠KDO+∠DKT,然后结合角平分线的性质可得:2∠KTO3∠GEH=∠GEH+∠EKG,最后由直角三角形的两锐角互余可得结论.
解:(1)(1)∵![]() ,
,
∴a2=0,(b+1)2=0,
∴a=2,b=1,
∵△ABC的面积为3,
∴S△ABC=![]() ABBC=3,
ABBC=3,
即![]() ×(m)×(2+1)=3,m=2,
×(m)×(2+1)=3,m=2,
故答案为:2,1,2;
(2)依题意有![]() 和
和![]() 都是直角三角形
都是直角三角形
∴![]()
∴![]()
![]()
![]()
∴![]()
(3)设![]() 交
交![]() 轴于点
轴于点![]() ,依题意有:
,依题意有:![]() 轴,
轴,
∴![]()
![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]() ,
,
∴所求![]() 的值是
的值是![]() .
.


科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0和-2;乙袋中有3个完全相同的小球,分别标有数字-2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求点Q在x轴上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直线L与x轴、y轴分别交于点B、A两点,且A、B两点的坐标分别为A(0,3),B(-4,0).
(1)请求出直线L的函数解析式;
(2)点P在坐标轴上,且△ABP的面积为12,求点P的坐标;
(3)点C为直线AB上一个动点,是否存在使点C到x轴的距离为1.5若存在请直接写出该点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,点C、D分别在边OA、OB上的点.连接AD,BC,点H为BC中点,连接OH.
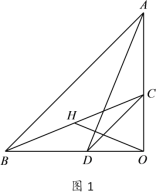
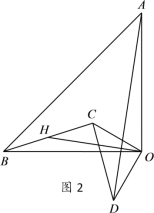
(1)如图1,求证:OH=![]() AD,OH⊥AD;
AD,OH⊥AD;
(2)将△COD绕点O旋转到图2所示位置时,⑴中结论是否仍成立?若成立,证明你的结论;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪计划中考后参加“我的中国梦”夏令营活动,需要一名家长陪同,爸爸、妈妈用猜拳的方式确定由谁陪同,即爸爸、妈妈随机做出“石头”、 “剪刀”“布” 三种手势中的一种,规定:“石头”胜“剪刀”,“剪刀” 胜“布”,“布” 胜“石头”,手势相同,不分胜负.
(1)爸爸一次出“石头”的概率是多少?
(2)妈妈一次获胜的概率是多少?请用列表或画树状图的方法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧交AN于点C,交AB于点D;②分别以C,D为圆心,以大于![]() CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为_____.
CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
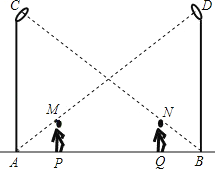
【题目】如图,王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行12m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6m,两个路灯的高度都是9.6m.
(1)求两个路灯之间的距离;
(2)当王华同学走到路灯BD处时,他在路灯AC下的影子长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作题
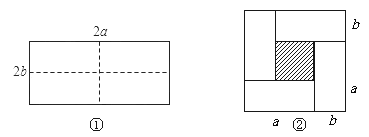
(1)如图①所示是一个长为2a,宽为2b的矩形,若把此图沿图中虚线用剪刀均分为四块小长方形,然后按图②的形状拼成一个正方形,请问:这两个图形的 不变.图②中阴影部分的面积用含a、b的代数式表示为_________________;
(2)由(1)的探索中,可得到的结论是:在周长一定的矩形中,___________时,面积最大;
(3)若一矩形的周长为36 cm,则当边长为多少时,该图形的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)把数轴补充完整.
(2)在数轴上表示下列各数.
(3)用“<”连接起来. .
(4)﹣|﹣2|与﹣4之间的距离是 .
3![]() ,﹣4,﹣(﹣1.5),﹣|﹣2|
,﹣4,﹣(﹣1.5),﹣|﹣2|
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com