
【题目】如图直线L与x轴、y轴分别交于点B、A两点,且A、B两点的坐标分别为A(0,3),B(-4,0).
(1)请求出直线L的函数解析式;
(2)点P在坐标轴上,且△ABP的面积为12,求点P的坐标;
(3)点C为直线AB上一个动点,是否存在使点C到x轴的距离为1.5若存在请直接写出该点的坐标.
【答案】(1)y=0.75x+3;(2)点P的坐标为(4,0)或(-12,0)或(0,3)或(0,9);(3)存在点C到x轴的距离为1.5,其坐标是(-2,1.5)或(-6,-1.5).
【解析】
(1)设直线L的解析式为y=kx+b(k≠0),把A,B代入求解即可;
(2)根据S△ABP的面积为12,分成①当P点在x轴上时,②当P点在y轴上时,两种情况讨论即可;
(3)假设存在点C(x,±1.5)到x轴的距离为1.5,将点C代入直线L的解析式求解判断即可.
解:(1)设直线L的解析式为y=kx+b(k≠0),
把A(0,3),B(-4,0)代入得![]() ,
,
解得![]() ,
,
∴解析式为:y=0.75x+3;
(2)∵A(0,3),B(-4,0),
∴|OA|=3,|OB|=4,
①当P点在x轴上时S△ABP=![]() ·|OB|·|AP|=
·|OB|·|AP|=![]() ×3·|AP|=12,
×3·|AP|=12,
解得:|AP|=8,
∴可得点P的坐标为:(4,0)或(-12,0),
②当P点在y轴上时S△ABP=![]() ·|OA|·|BP|=
·|OA|·|BP|=![]() ×4·|BP|=12,
×4·|BP|=12,
解得:|BP|=6,
∴可得点P的坐标为:(0,3)或(0,9),
综上:点P的坐标为(4,0)或(-12,0)或(0,3)或(0,9);
(3)假设存在点C(x,±1.5)到x轴的距离为1.5,则点C(x,±1.5)满足方程y=0.75x+3,
①当C(x,1.5)时,1.5=0.75x+3,
解得x=-2,
∴点C(-2,1.5)存在,
②当C(x,-1.5)时,-1.5=0.75x+3,
解得x=-6,
∴C(-6,-1.5)存在,
∴存在点C到x轴的距离为1.5,其坐标是(-2,1.5)或(-6,-1.5).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() .点C在点
.点C在点![]() 的右侧,
的右侧,![]() ,
,![]() 平分么
平分么![]() ,平分
,平分![]() 所在的直线交于点
所在的直线交于点![]() ,点
,点![]() 在
在![]() 之间。
之间。
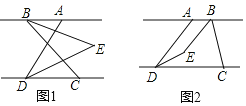
(1)如图1,点![]() 在点A的左侧,若
在点A的左侧,若![]() ,求
,求![]() 的度数?
的度数?
(2)如图2,点![]() 在点A的右侧,若
在点A的右侧,若![]() ,直接写出
,直接写出![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,分别沿矩形纸片ABCD和正方形EFGH纸片的对角线AC,EG剪开,拼成如图2所示的平行四边形KLMN,若中间空白部分恰好是正方形OPQR.
(1)若AB=m,BC=n,用含m、n的代数式表示正方形EFGH的边长;
(2)若正方形EFGH的面积为25,求平行四边形KLMN的面积;
(3)平行四边形KLMN是否能为菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小李8时骑自行车从家里出发,到野外郊游,16时回到家里.他离家的距离s(千米)与时间t(时)之间的函数关系可以用图中的折线表示.现有如下信息:
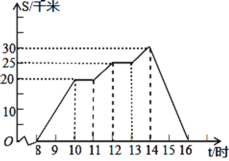
(1)小李到达离家最远的地方的时间是14时;
(2)小李第一次休息时间是10时;
(3)11时到12时,小李骑了5千米;
(4)返回时,小李的平均车速是10千米/时.
其中,正确的信息有___________________(填番号).
查看答案和解析>>
科目:初中数学 来源: 题型:
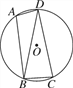
【题目】如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对各种球类运动的喜爱程度,小明采取随机抽样的方法对他所在学校的部分学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一种项目),对调查结果进行统计后,绘制了下面的统计图(1)和图(2).
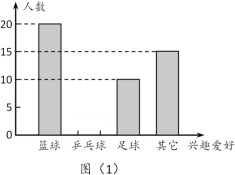

(1)此次被调查的学生共有___人,m=_____;
(2)求喜欢“乒乓球”的学生的人数,并将条形统计图补充完整;
(3)若该校有2000名学生,估计全校喜欢“足球”的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知![]() ,
,![]() ,
,![]()
![]() 且
且![]() ,
,![]() 的面积为3.
的面积为3.
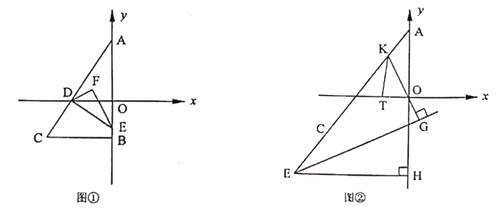
(1)直接写出![]() ,
,![]() ,
,![]() .
.
(2)如图①,设![]() 交
交![]() 轴于
轴于![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 、
、![]() 的角平分线交于点
的角平分线交于点![]() ,求
,求![]() 的大小.
的大小.
(3)如图②,点![]() 是
是![]() 延长线上动点,
延长线上动点,![]() 轴于点
轴于点![]() ,
,![]() 平分
平分![]() ,直线
,直线![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,
,![]() 平分
平分![]() 交
交![]() 轴于
轴于![]() 点,求
点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式![]() <
<![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
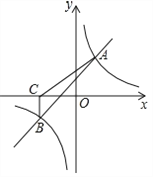
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com