
【题目】如图1,分别沿矩形纸片ABCD和正方形EFGH纸片的对角线AC,EG剪开,拼成如图2所示的平行四边形KLMN,若中间空白部分恰好是正方形OPQR.
(1)若AB=m,BC=n,用含m、n的代数式表示正方形EFGH的边长;
(2)若正方形EFGH的面积为25,求平行四边形KLMN的面积;
(3)平行四边形KLMN是否能为菱形?请说明理由.

【答案】(1)![]() ;(2)50;(3)不能,理由见解析.
;(2)50;(3)不能,理由见解析.
【解析】
(1)设正方形![]() 的边长为
的边长为![]() ,则:
,则:![]() ,
,![]() ,根据四边形EFGH是正方形,得到
,根据四边形EFGH是正方形,得到![]() ,即有
,即有![]() ,
,![]() ,利用
,利用![]() 可以得到结果;
可以得到结果;
(2)设正方形![]() 的边长为
的边长为![]() ,根据正方形
,根据正方形![]() 面积为25,可得
面积为25,可得![]() ,
,![]() ,据此可得平行四边形KLMN的面积.
,据此可得平行四边形KLMN的面积.
(3)利用反证法,假设是菱形,则![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,可求出m=n,则小正方形ROPQ边长为0,与题目描述相矛盾,所以假设不成立,不是菱形.
,可求出m=n,则小正方形ROPQ边长为0,与题目描述相矛盾,所以假设不成立,不是菱形.
(1)设正方形![]() 的边长为
的边长为![]() ,
,
则:![]() ,
,![]() ,、
,、
∵四边形EFGH是正方形,
∴![]() ,即有
,即有![]()
∴![]() ,
,
∴![]()
(2)设正方形![]() 的边长为
的边长为![]() ,
,
∵正方形![]() 面积为25,
面积为25,
∴正方形![]() 边长为5,
边长为5,
∴![]() ,
,![]() ,
,
∴平行四边形KLMN的面积![]() .
.
(3)结论:不能.
证明:假设是菱形,则![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,
,
于是有![]() ,
,
则![]() ,即
,即![]() ,则m=n,
,则m=n,
则小正方形ROPQ边长为0,与题目描述相矛盾.所以假设不成立,不是菱形.


科目:初中数学 来源: 题型:
【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0和-2;乙袋中有3个完全相同的小球,分别标有数字-2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求点Q在x轴上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D,E分别是AB,AC的中点,点G,F在BC边上(均不与端点重合),DG∥EF.将△BDG绕点D顺时针旋转180°,将△CEF绕点E逆时针旋转180°,拼成四边形MGFN,则四边形MGFN周长l的取值范围是___________.
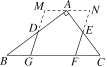
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.
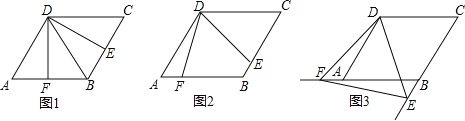
(1)继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由;
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)连EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地,(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.快车到达甲地时,慢车距离甲地__米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直线L与x轴、y轴分别交于点B、A两点,且A、B两点的坐标分别为A(0,3),B(-4,0).
(1)请求出直线L的函数解析式;
(2)点P在坐标轴上,且△ABP的面积为12,求点P的坐标;
(3)点C为直线AB上一个动点,是否存在使点C到x轴的距离为1.5若存在请直接写出该点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,点C、D分别在边OA、OB上的点.连接AD,BC,点H为BC中点,连接OH.
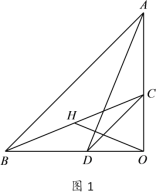
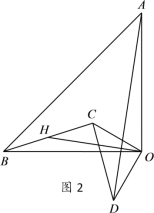
(1)如图1,求证:OH=![]() AD,OH⊥AD;
AD,OH⊥AD;
(2)将△COD绕点O旋转到图2所示位置时,⑴中结论是否仍成立?若成立,证明你的结论;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
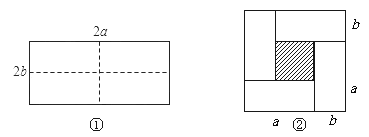
【题目】操作题
(1)如图①所示是一个长为2a,宽为2b的矩形,若把此图沿图中虚线用剪刀均分为四块小长方形,然后按图②的形状拼成一个正方形,请问:这两个图形的 不变.图②中阴影部分的面积用含a、b的代数式表示为_________________;
(2)由(1)的探索中,可得到的结论是:在周长一定的矩形中,___________时,面积最大;
(3)若一矩形的周长为36 cm,则当边长为多少时,该图形的面积最大?最大面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com