练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

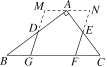
    【题目】如图，在Rt△ABC中，∠BAC＝90°，AB＝4，AC＝3，点D，E分别是AB，AC的中点，点G，F在BC边上(均不与端点重合)，DG∥EF.将△BDG绕点D顺时针旋转180°，将△CEF绕点E逆时针旋转180°，拼成四边形MGFN，则四边形MGFN周长l的取值范围是___________.

    【答案】≤l＜13

    【解析】如图,连接DE,作AH⊥BC于H.

    在Rt△ABC中, ∵∠BAC=90°AB＝4，AC＝3，,

    ,

    ,

    ,

    , ,

    , ,

    ,

    ∴四边形DGEF是平行四边形,

    ,

    根据题意,,

    ∴四边形MNFG是平行四边形,

    ∴当MG=NF=AH时,可得四边形MNFG周长的最小值= ,

    当G与B重合时可得周长的最大值为13,

    ∵G不与B重合,

    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】自学下面材料后，解答问题。

    分母中含有未知数的不等式叫分式不等式。如： <0等。那么如何求出它们的解集呢?

    根据我们学过的有理数除法法则可知：两数相除，同号得正，异号得负。其字母表达式为：

    若a>0,b>0,则>0;若a<0,b<0,则>0；

    若a>0,b<0,则<0;若a<0,b>0,则<0.

    反之：若>0,则 或 ，

    （1）若<0，则___或___.

    （2）根据上述规律,求不等式 >0的解集.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

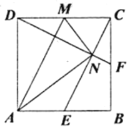
    【题目】如图，E，F，M分别是正方形ABCD三边的中点，CE与DF交于N，连接AM，AN，MN对于下列四个结论：①AM∥CE；②DF⊥CE；③AN=BC；④∠AND=∠CMN． 其中错误的是（ ）

    A.①B.②C.③D.④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知,平分，点、、分别是射线、、上的动点（、、不与点重合），连接交射线于点，设.

    （1）如图1，若，则：

    ①的度数为

    ②当时， ，当时，

    （2）如图2，若，则是否存在这样的的值，使得中有两个想等的角？若存在，求出的值；若不存在，说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′，则图中阴影部分的面积为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将两块三角尺AOB与COD的直角顶点O重合在一起，若∠AOD=4∠BOC，OE为∠BOC的平分线，则∠DOE的度数为（　　）

    A. 36° B. 45° C. 60° D. 72°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，分别沿矩形纸片ABCD和正方形EFGH纸片的对角线AC，EG剪开，拼成如图2所示的平行四边形KLMN，若中间空白部分恰好是正方形OPQR．

    （1）若AB=m，BC=n，用含m、n的代数式表示正方形EFGH的边长；

    （2）若正方形EFGH的面积为25，求平行四边形KLMN的面积；

    （3）平行四边形KLMN是否能为菱形？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

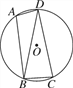
    【题目】如图，已知四边形ABCD内接于圆O，连接BD，∠BAD＝105°，∠DBC＝75°.

    (1)求证：BD＝CD；

    (2)若圆O的半径为3，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（分）周末，小英与她的父亲、母亲计划从西安外出旅游，初步选择了位于西安东线的景点：兵马俑， ：华山，以及位于西线的景点：太白山， ：法门寺， ：杨凌现代农业示范园．由于时间仓促，他们只能去其中的两个景点，并且希望两个景点能位于一条线路上．到底去哪两个景点，三人意见不统一．在这种情况下，小英父亲建议，用小英学过的摸卡片游戏来决定．规则如下：在五个背面完全相同的卡片上写上五个景点的代号，然后洗匀，背面朝上放在桌面上，让小英随机摸出一张，不放回，然后让小英母亲再随机摸出一张．照上面的规则，请你解答下列问题：

    （）己知小英的理想旅游景点是兵马俑，求小英摸出写有的卡片的概率．

    （）求小英和母亲摸出的景点位于一条线上（东线或西线）的概率．

    查看答案和解析>>

    同步练习册答案