
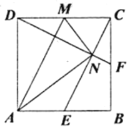
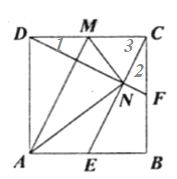
【题目】如图,E,F,M分别是正方形ABCD三边的中点,CE与DF交于N,连接AM,AN,MN对于下列四个结论:①AM∥CE;②DF⊥CE;③AN=BC;④∠AND=∠CMN. 其中错误的是( )
A.①B.②C.③D.④
【答案】D
【解析】
证四边形AECM为平行四边形得①正确,证![]() ≌
≌![]() (SAS)易得②正确,证AM垂直平分DN得到③正确,而推导不出∠AND=∠CMN,故④错误
(SAS)易得②正确,证AM垂直平分DN得到③正确,而推导不出∠AND=∠CMN,故④错误
解:∵正方形ABCD,M,E分别为DC,AB的中点,∴CM∥AE,CM=AE,∴四边形AECM为平行四边形,∴AM//CE,①正确;∵CD=BC,∠DCB=∠CBE=90°,CF=BE,∴![]() ≌
≌![]() (SAS),∴∠1=∠2,∵∠2+∠3=90°,∴∠1+∠3=90°,∴DF⊥CE,∴②正确;∵Rt
(SAS),∴∠1=∠2,∵∠2+∠3=90°,∴∠1+∠3=90°,∴DF⊥CE,∴②正确;∵Rt![]() ,M为斜边DC的中点,∴DM=CM=MN,∵AM//CE,DF⊥CE,∴AM⊥DF,∴AM垂直平分DN,∴AD=AN=BC,∴③正确,∴∠AND=∠ADN,∵∠1+∠AND=90°,∠1+∠3=90°,∴∠AND=∠3=∠MNC≠∠CMN,故④错误.故答案为D.
,M为斜边DC的中点,∴DM=CM=MN,∵AM//CE,DF⊥CE,∴AM⊥DF,∴AM垂直平分DN,∴AD=AN=BC,∴③正确,∴∠AND=∠ADN,∵∠1+∠AND=90°,∠1+∠3=90°,∴∠AND=∠3=∠MNC≠∠CMN,故④错误.故答案为D.


科目:初中数学 来源: 题型:
【题目】(![]() 分)如图,管中放置着三根同样的绳子
分)如图,管中放置着三根同样的绳子![]() ,
, ![]() ,
, ![]() .
.
(![]() )小明从
)小明从![]() 这三根绳子中随机选一根,恰好选中绳子
这三根绳子中随机选一根,恰好选中绳子![]() 的概率是__________.
的概率是__________.
(![]() )小明先从左端
)小明先从左端![]() ,
, ![]() ,
, ![]() 三个绳头中随机选两个打一个结,再从右端
三个绳头中随机选两个打一个结,再从右端![]() ,
, ![]() ,
, ![]() 三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.
三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
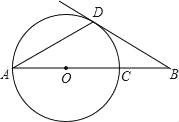
【题目】如图,点B在⊙O的直径AC的延长线上,点D在⊙O上,AD=DB,∠B=30°,若⊙O的半径为4.
(1)求证:BD是⊙O的切线;
(2)求CB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
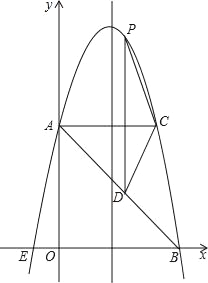
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形![]() 中,在对角线
中,在对角线![]() 上取不同的两点
上取不同的两点![]() (点B、E、F、D依次排列),下列条件中,能得出四边形
(点B、E、F、D依次排列),下列条件中,能得出四边形![]() 一定为平行四边形的是_____________.(A. BE=DF;B. AE=CF C. AE∥CF;D. ∠BAE=∠DCF)
一定为平行四边形的是_____________.(A. BE=DF;B. AE=CF C. AE∥CF;D. ∠BAE=∠DCF)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0和-2;乙袋中有3个完全相同的小球,分别标有数字-2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求点Q在x轴上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D,E分别是AB,AC的中点,点G,F在BC边上(均不与端点重合),DG∥EF.将△BDG绕点D顺时针旋转180°,将△CEF绕点E逆时针旋转180°,拼成四边形MGFN,则四边形MGFN周长l的取值范围是___________.
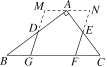
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,点C、D分别在边OA、OB上的点.连接AD,BC,点H为BC中点,连接OH.
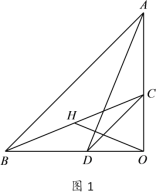
(1)如图1,求证:OH=![]() AD,OH⊥AD;
AD,OH⊥AD;
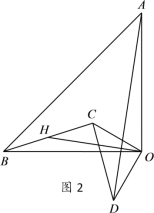
(2)将△COD绕点O旋转到图2所示位置时,⑴中结论是否仍成立?若成立,证明你的结论;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com