
【题目】如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒![]() ,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.
,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.


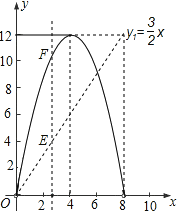
(1)求y1与x的函数关系,并在图2中画出y1的图象;
(2)如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;
(3)在图2中,点G是x轴正半轴上一点(0<OG<6),过G作EF垂直于x轴,分别交y1、y2于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.
【答案】(1)![]() .图象如图所示:
.图象如图所示:
(2)点P的速度每秒![]() 厘米,AC=12厘米;
厘米,AC=12厘米;
(3)①表示△PCQ与△DCQ的面积差(或△PDQ面积);②![]()
【解析】
试题分析:(1)已知了CD=3,根据Q点的速度可以用时间x表示出CQ的长,可根据三角形的面积计算公式得出y1,x的函数关系式;
(2)可先求出y2的函数式,然后根据其顶点坐标来确定k的取值.已知了P点走完AC用时8s,因此AC=8k,而AP=kx,CQ=x,那么可根据三角形的面积公式列出关于y2,x的函数关系式,进而可根据顶点坐标求出k的值;
(3)EF其实就是y2-y1,也就是三角形PCQ和CDQ的面积差即三角形PDQ的面积.得出EF的函数关系式后,根据自变量的取值以及函数的性质即可求出EF的最大值.
(1)∵![]() ,CD=3,CQ=x,
,CD=3,CQ=x,
∴![]() .图象如图所示:
.图象如图所示:

(2)![]() ,CP=8k-xk,CQ=x,
,CP=8k-xk,CQ=x,
∴![]() .
.
∵抛物线顶点坐标是(4,12),
∴![]() .解得
.解得![]()
则点P的速度每秒![]() 厘米,AC=12厘米;
厘米,AC=12厘米;
(3)①观察图象,知线段的长EF=y2-y1,表示△PCQ与△DCQ的面积差(或△PDQ面积)
②由(2)得 ![]() .
.
∵EF=y2-y1,
∴EF=![]() ,
,
∵二次项系数小于0,
∴在![]() 范围,当
范围,当![]() 时,
时,![]() 最大.
最大.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2 , 使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3 , 使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是 . 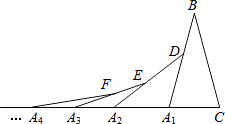
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示的方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过2017次运动后,动点P的坐标为 . 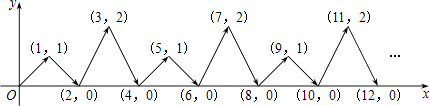
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一块含45°角的三角板的直角顶点靠在长尺(两边a∥b)的一边b上,若∠1=30°,则三角板的斜边与长尺的另一边a的夹角∠2的度数为( ) 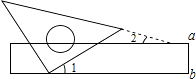
A.10°
B.15°
C.30°
D.35°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在五边形ABCDE中,∠A+∠B+∠E=α,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( ) 
A.![]() α﹣90°
α﹣90°
B.90° ![]()
C.![]()
D.540° ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列文字:
我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2 .
请解答下列问题: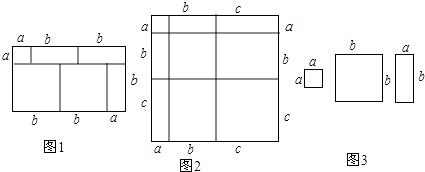
(1)写出图2中所表示的数学等式;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=12,ab+bc+ac=42,求a2+b2+c2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片,请利用所给的纸片拼出一个几何图形,使得用两种不同的方法计算它的面积时,能够得到数学公式:2a2+7ab+3b2=(a+3b)(2a+b).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com