
【题目】(1)解不等式组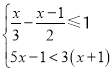 ,并求出所有整数解的和.
,并求出所有整数解的和.
(2)分解因式:![]()
(3)解方程:![]() .
.
(4)先化简,再求值: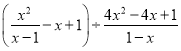 ,其中
,其中![]() .
.
科目:初中数学 来源: 题型:
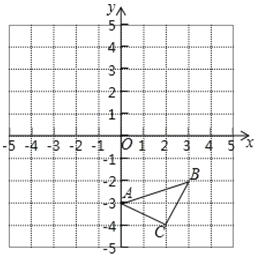
【题目】如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(0,-3),B(3,-2),C(2,-4).
(1)在图中作出△ABC关于x轴对称的△A1B1C1.
(2)点C1的坐标为: .
(3)△ABC的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
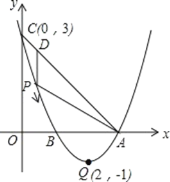
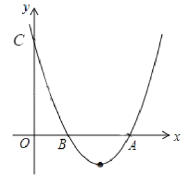
【题目】如图,已知抛物线 y=ax2+bx+c(a≠0)的顶点坐标为 Q(2,﹣1),且与 y 轴交于点 C(0,3), 与 x 轴交于 A、B 两点(点 A 在点 B 的右侧),点 P 是抛物线上的一动点,从点 C 沿抛物线向 点 A 运动(点 P 与 A 不重合),过点 P 作 PD∥y 轴,交 AC 于点 D.
(1)求该抛物线的函数关系式及 A、B 两点的坐标;
(2)求点 P 在运动的过程中,线段 PD 的最大值;
(3)若点 P 与点 Q 重合,点 E 在 x 轴上,点 F 在抛物线上,问是否存在以 A,P,E,F 为顶 点的平行四边形?若存在,直接写出点 F 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.

查看答案和解析>>
科目:初中数学 来源: 题型:
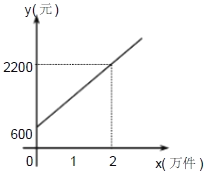
【题目】某公司市场营销部的营销员有部分收入按照业务量或销售额提成,即多卖多得.营销员的月提成收入![]() (元)与其每月的销售量
(元)与其每月的销售量![]() (万件)成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题:
(万件)成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题:
(1)求出![]() (元)与
(元)与![]() (万件)(其中
(万件)(其中![]() )之间的函数关系式;
)之间的函数关系式;
(2)已知该公司营销员李平12月份的销售量为1.2万件,求李平12月份的提成收入.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com