
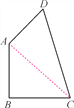
【题目】如图,在四边形ABCD中,AB=BC=1,CD=![]() ,DA=1,且∠B=90°.求:
,DA=1,且∠B=90°.求:
(1)∠BAD的度数;
(2)四边形ABCD的面积(结果保留根号).
【答案】(1)135°;(2)![]()
【解析】试题分析:(1)由于AB=BC=1,且∠B=90°根据勾股定理即可求出AC的长度,而CD=![]() ,DA=1,利用勾股定理的逆定理即可证明△ACD是直角三角形,由此即可求出∠BAD的度数;
,DA=1,利用勾股定理的逆定理即可证明△ACD是直角三角形,由此即可求出∠BAD的度数;
(2)首先把求四边形ABCD的面积分割为求△ABC和△ACD的面积,然后利用三角形的面积公式可以分别求出这两个三角形的面积,最后就可以求出四边形ABCD的面积.
试题解析:(1)∵AB=BC=1,且∠B=90°,
∴∠BAC=45°,AC=![]() ,
,
而CD=![]() ,DA=1,
,DA=1,
∴CD2=AD2+AC2,
∴△ACD是直角三角形,即∠DAC=90°,
∴∠BAD=∠BAC+∠DAC=135°;
(2)∵S四边形ABCD=S△ABC+S△ACD,
而S△ABC=![]() AB×BC=
AB×BC=![]() ,
,
S△ACD=![]() AD×CD=
AD×CD=![]() ,
,
∴S四边形ABCD=S△ABC+S△ACD=![]()
.


科目:初中数学 来源: 题型:
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+![]() =(1+
=(1+![]() )2.善于思考的小明进行了以下探索:
)2.善于思考的小明进行了以下探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() .
.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分别表示a、b,得:a= ,b= ;
)2,用含m、n的式子分别表示a、b,得:a= ,b= ;
(2)利用探索的结论,找一组正整数a、b、m、n (a、b都不超过20)
填空: + ![]() =( +
=( + ![]() )2;
)2;
(3)若a+6![]() =(m+n
=(m+n![]() )2,且a、m、n均为正整数,求a的值?
)2,且a、m、n均为正整数,求a的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,- ![]() )三点.
)三点.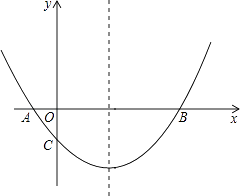
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校住校生宿舍有大小两种寝室若干间,据统计该校高一年级男生740人,使用了55间大寝室和50间小寝室,正好住满;女生730人,使用了大寝室50间和小寝室55间,也正好住满.求该校的大小寝室每间各住多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证△BED≌△CFD.
(2)已知EC=6,AC=10,求BE.
(3)当∠C=45°时,判断△DFC的周长与线段AC长度的关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队承包一项工程,如果甲工程队单独施工,恰好如期完成;如果乙工程队单独施工就要超过6个月才能完成,现在甲、乙两队先共同施工4个月,剩下的由乙队单独施工,则恰好如期完成.
(1)问原来规定修好这条公路需多少长时间?
(2)现要求甲、乙两个工程队都参加这项工程,但由于受到施工场地条件限制,甲、乙两工程队不能同时施工.已知甲工程队每月的施工费用为4万元,乙工程队每月的施工费用为2万元.为了结算方便,要求:甲、乙的施工时间为整数个月,不超过15个月完成.当施工费用最低时,甲、乙各施工了多少个月?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com