
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证△BED≌△CFD.
(2)已知EC=6,AC=10,求BE.
(3)当∠C=45°时,判断△DFC的周长与线段AC长度的关系,并说明理由.

【答案】(1)见解析;(2)2;(3)△DFC的周长等于AC的长度,理由见解析.
【解析】
(1)由已知条件根据“HL”即可证得△BED≌△CFD;
(2)由已知易得AE=8,由(1)中所得△BED≌△CFD可得DE=DF,结合AD=AD,∠AED=∠AFD=90°可得△AED≌△AFD,由此可得AE=AF=AC-CF,再结合BE=CF即可得到AE=AC-BE,从而可得BE=AC-AE=10-8=2;
(3)当∠C=45°时,易得△AEC是等腰直角三角形,结合(2)中所得AE=AF可得CE=AE=AF,结合DF=DE即可得到△DCF的周长=DC+DF+FC=DC+DE+FC=CE+FC=AF+FC=AC.
(1)∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°.
∵在Rt△BED和Rt△CFD中,BE=CF,BD=CD,
∴Rt△BED≌ Rt△CFD(HL);
(2)∵DE⊥AE,EC=6,AC=10,
∴在Rt△AEC中,AE=![]() ,
,
由(1)中所得Rt△BED≌ Rt△CFD可得DE=DF,
∵在△AED和△AFD中,DE=DF,AD=AD,∠E=∠AFD=90°,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF ,
又∵AF=AC-CF,
∴AE=AC-CF ,
又∵BE=CF ,
∴AE=AC-B E ,即8=10-BE ,
∴BE=2 ;
(3)△DFC的周长等于AC的长度,理由如下:
∵∠C=45°,∠E=90°,
∴△AEC为等腰直角三角形,
∴AE=EC,
∵由(2)可知AE=AF,
∴AF=EC,
又∵DE=DF,
∴△DFC的周长=CD+DF+FC=CD+DE+FC=CE+FC=AF+FC=AC.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
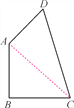
【题目】如图,在四边形ABCD中,AB=BC=1,CD=![]() ,DA=1,且∠B=90°.求:
,DA=1,且∠B=90°.求:
(1)∠BAD的度数;
(2)四边形ABCD的面积(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,射线
,射线![]() 分别和直线
分别和直线![]() 交于点
交于点![]() ,射线
,射线![]() 分别和直线
分别和直线![]() 交于点
交于点![]() ,点
,点![]() 在射线
在射线![]() 上运动(
上运动(![]() 点与
点与![]() 三点不重合),设
三点不重合),设![]() ,
,![]() ,
,![]() .
.

(1)如果点![]() 在
在![]() 两点之间运动时,
两点之间运动时,![]() 之间有何数量关系?请说明理由;
之间有何数量关系?请说明理由;
(2)如果点![]() 在
在![]() 两点之外运动时,
两点之外运动时,![]() 之间有何数量关系?(只需写出结论,不必说明理由)
之间有何数量关系?(只需写出结论,不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:_____________,使△AEH≌△CEB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线AB∥CD
(1)如图1,点E在直线BD的左侧,猜想∠ABE、∠CDE、∠BED的数量关系,并证明你的结论;
(2)如图2,点E在直线BD的左侧,BF、DF分别平分∠ABE、∠CDE,猜想∠BFD和∠BED的数量关系,并证明你的结论;
(3)如图3,点E在直线BD的右侧,BF、DF分别平分∠ABE、∠CDE;那么第(2)题中∠BFD和∠BED的数量关系的猜想是否仍成立?如果成立,请证明;如果不成立,请写出你的猜想,并证明.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF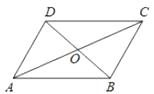
(1)根据题意,补全原形;
(2)求证:BE=DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:
不成立,但有些数可以使得它成立,例如: ![]() .我们称使得
.我们称使得![]() 成立的一对数
成立的一对数![]() ,
, ![]() 为“相伴数对”,记为
为“相伴数对”,记为![]() .
.
(1)若![]() 是“相伴数对”,求
是“相伴数对”,求![]() 的值;
的值;
(2)写出一个“相伴数对” ![]() ,其中
,其中![]() 且
且![]() ;
;
(3)若![]() 是“相伴数对”,求代数式
是“相伴数对”,求代数式![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com