
【题目】如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连结CE绕点C顺时针旋转110°,得到线段CF,连结BE,DF,若∠E=86°,求∠F的度数.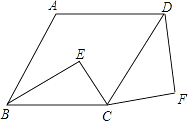
【答案】解:∵菱形ABCD,
∴BC=CD,∠BCD=∠A=110°,
由旋转的性质知,CE=CF,∠ECF=∠BCD=110°,
∴∠BCE=∠DCF=110°﹣∠DCE,
在△BCE和△DCF中, 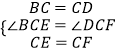 ,
,
∴△BCE≌△DCF,
∴∠F=∠E=86°.
【解析】由菱形的性质得出邻边相等,对角相等,旋转的性质可知CE=CF,证得△BCE≌△DCF,∠F可转化为∠E的度数.
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于点和A(﹣1,0)和点B(4,0),与y轴交于点C(0,2).
(1)求抛物线解析式;
(2)点P是抛物线BC段上一点,PD⊥BC,PE∥y轴,分别交BC于点D、E.当DE= ![]() 时,求点P的坐标;
时,求点P的坐标;
(3)M是平面内一点,将符合(2)条件下的△PDE绕点M沿逆时针方向旋转90°后,点P,D,E的对应点分别是P′、D′、E′.设P′E′的中点为N,当抛物线同时经过D′与N时,求出D′的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画出直线y=![]() x-1的图象,利用图象求:
x-1的图象,利用图象求:
(1)当x≥2时,y的取值范围;
(2)当y<0时,x的取值范围;
(3)当-1≤y≤2时,对应x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述:①如果a是非负数,则![]() ;②“
;②“![]() 减去10不大于2”表示为
减去10不大于2”表示为![]() ;③“
;③“![]() 的倒数超过10”表示为
的倒数超过10”表示为![]() ;④“a,b两数的平方和为正数”表示为
;④“a,b两数的平方和为正数”表示为![]() ;其中正确的个数是( )
;其中正确的个数是( )
A. 2 个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学老师在课堂上提出一个问题:“通过探究知道:![]() ≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用
≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用![]() ﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:
﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:
(1)![]() 的小数部分是a,
的小数部分是a,![]() 的整数部分是b,求a+2b﹣
的整数部分是b,求a+2b﹣![]() 的值.
的值.
(2)已知6+![]() =x+y,其中x是一个整数,0<y<1,求2x+(y﹣
=x+y,其中x是一个整数,0<y<1,求2x+(y﹣![]() )2018的值.
)2018的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的不等式表示下列不等关系:
(1)x减去6大于12;
(2)x的2倍与5的差是负数;
(3)x的3倍与4的和是非负数;
(4)y的5倍与9的差不大于![]() ;
;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG= ![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
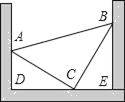
【题目】如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com