

分析 (1)先证明△CDE≌△BDF,即可得出结论;
(2)不成立;同(1)得:△DEC≌△DBF,得出S△DEF=S五边形DBFEC=S△CFE+S△DBC=S△CFE+$\frac{1}{2}$S△ABC.
解答 解:(1)连接CD;如图2 所示:
所示:
∵AC=BC,∠ACB=90°,D为AB中点,
∴∠B=45°,∠DCE=$\frac{1}{2}$∠ACB=45°,CD⊥AB,CD=$\frac{1}{2}$AB=BD,
∴∠DCE=∠B,∠CDB=90°,
∵∠EDF=90°,
∴∠1=∠2,
在△CDE和△BDF中,
$\left\{\begin{array}{l}{∠1=∠2}\\{CD=BD}\\{∠DCE=∠B}\end{array}\right.$,
∴△CDE≌△BDF(ASA),
∴S△DEF+S△CEF=S△ADE+S△BDF=$\frac{1}{2}$S△ABC;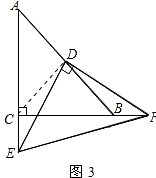 (2)不成立;${S}_{△DEF}-{S}_{△CEF}=\frac{1}{2}{S}_{△ABC}$;理由如下:连接CD,如图3所示:
(2)不成立;${S}_{△DEF}-{S}_{△CEF}=\frac{1}{2}{S}_{△ABC}$;理由如下:连接CD,如图3所示:
同(1)得:△DEC≌△DBF,∠DCE=∠DBF=135°
∴S△DEF=S五边形DBFEC,
=S△CFE+S△DBC,
=S△CFE+$\frac{1}{2}$S△ABC,
∴S△DEF-S△CFE=$\frac{1}{2}$S△ABC.
∴S△DEF、S△CEF、S△ABC的关系是:S△DEF-S△CEF=$\frac{1}{2}$S△ABC.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的性质、图形面积的求法;证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:填空题
 如图,把一张矩形纸片ABCD折叠成一个四边形AECD,已知CD=3,折痕CE长为2,则四边形AECD的面积为3$\sqrt{2}$-1..
如图,把一张矩形纸片ABCD折叠成一个四边形AECD,已知CD=3,折痕CE长为2,则四边形AECD的面积为3$\sqrt{2}$-1..查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,sinB=$\frac{1}{3}$,AD=CD=1.
如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,sinB=$\frac{1}{3}$,AD=CD=1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,点D在边AB上,AD=20cm,BD=16cm,BC=24cm,点E在边AC上,且△ADE与△BCD相似.
如图,在△ABC中,点D在边AB上,AD=20cm,BD=16cm,BC=24cm,点E在边AC上,且△ADE与△BCD相似.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,过⊙C上一点P作⊙C的切线l.当入射光线照射在点P处时,产生反射,且满足:反射光线与切线l的夹角和入射光线与切线l的夹角相等,点P称为反射点.规定:光线不能“穿过”⊙C,即当入射光线在⊙C外时,只在圆外进行反射;当入射光线在⊙C内时,只在圆内进行反射.特别地,圆的切线不能作为入射光线和反射光线.
在平面直角坐标系xOy中,过⊙C上一点P作⊙C的切线l.当入射光线照射在点P处时,产生反射,且满足:反射光线与切线l的夹角和入射光线与切线l的夹角相等,点P称为反射点.规定:光线不能“穿过”⊙C,即当入射光线在⊙C外时,只在圆外进行反射;当入射光线在⊙C内时,只在圆内进行反射.特别地,圆的切线不能作为入射光线和反射光线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
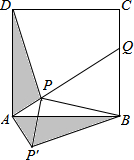 如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com