
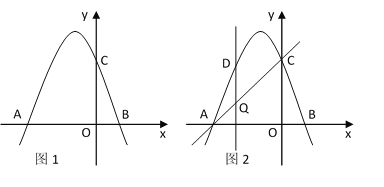
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпy=Љx2+bx+cНЛxжсгкЕуA(- 4ЃЌ0)КЭЕуBЃЌНЛyжсгкЕуC(0ЃЌ4)ЃЎ
(1)ЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
(2)ШчЭМ2ЃЌЩшЕуQЪЧЯпЖЮACЩЯЕФвЛЖЏЕуЃЌзїDQЁЭxжсЃЌНЛХзЮяЯпгкЕуDЃЌЕБЁїADCУцЛ§газюДѓжЕЪБЃЌдкХзЮяЯпЖдГЦжсЩЯеввЛЕуMЃЌЪЙDM+AMЕФжЕзюаЁЃЌЧѓГіДЫЪБMЕФзјБъЃЛ
(3)ЕуQдкжБЯпACЩЯЕФдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкЕуQЃЌЪЙЁїBQCЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌжБНгаДГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЁОД№АИЁП(1)![]() ЃЛ(2)ЕуMЕФзјБъЮЊM(
ЃЛ(2)ЕуMЕФзјБъЮЊM(![]() ЃЌ5)ЃЛ(3)ДцдкЃЌQ(
ЃЌ5)ЃЛ(3)ДцдкЃЌQ(![]() ЃЌ
ЃЌ![]() )Лђ(
)Лђ(![]() ЃЌ
ЃЌ![]() )Лђ(-3ЃЌ1)Лђ(
)Лђ(-3ЃЌ1)Лђ(![]() ).
).
ЁОНтЮіЁП
ЃЈ1ЃЉНЋA(- 4ЃЌ0)ЁЂC(0ЃЌ4)ДњШыy=Љx2+bx+cжаМДПЩЕУЃЛ
ЃЈ2ЃЉжБЯпACЕФНтЮіЪНЮЊЃК![]() ЃЌБэДяГіDQЕФГЄЖШЃЌМАЁїADCЕФУцЛ§ЃЌИљОнЖўДЮКЏЪ§ЕФаджЪЕУГіЁїADCУцЛ§ЕФзюДѓжЕЃЌДгЖјЕУГіDЕузјБъЃЌзїЕуDЙигкЖдГЦжсЖдГЦЕФЕуЃЌШЗЖЈЕуMЃЌЪЙDM+AMЕФжЕзюаЁЃЛ
ЃЌБэДяГіDQЕФГЄЖШЃЌМАЁїADCЕФУцЛ§ЃЌИљОнЖўДЮКЏЪ§ЕФаджЪЕУГіЁїADCУцЛ§ЕФзюДѓжЕЃЌДгЖјЕУГіDЕузјБъЃЌзїЕуDЙигкЖдГЦжсЖдГЦЕФЕуЃЌШЗЖЈЕуMЃЌЪЙDM+AMЕФжЕзюаЁЃЛ
ЃЈ3ЃЉЁїBQCЮЊЕШбќШ§НЧаЮЃЌдђБэДяГіШ§БпЃЌВЂЖдШ§БпНјааЗжРрЬжТлЃЌМЦЫуЕУГіQЕуЕФзјБъМДПЩ.
НтЃК(1)НЋA(- 4ЃЌ0)ЁЂC(0ЃЌ4)ДњШыy=Љx2+bx+cжаЕУ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
(2)жБЯпACЕФНтЮіЪНЮЊЃК![]()
ЩшQ(mЃЌm+4) ЃЌдђ D(mЃЌ![]() )
)
DQ=(![]() )- (m+4)=
)- (m+4)= ![]()
![]()
ЕБm=-2ЪБЃЌУцЛ§газюДѓжЕ
ДЫЪБЕуDЕФзјБъЮЊD(-2ЃЌ6)ЃЌDЕуЙигкЖдГЦжс![]() ЖдГЦЕФЕуD1(-1ЃЌ6)
ЖдГЦЕФЕуD1(-1ЃЌ6)
жБЯпAD1ЕФНтЮіЪНЮЊЃК![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ЫљвдЃЌЕуMЕФзјБъЮЊM(![]() ЃЌ5)
ЃЌ5)
(3)Ёп![]() ЃЌ
ЃЌ
ЁрЩшQ(t,t+4)ЃЌ
гЩ![]() ЕУ
ЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрB(1,0)ЃЌ
Ёр![]()
![]()
![]() ,
,
ЁїBQCЮЊЕШбќШ§НЧаЮ
ЂйЕБBC=QCЪБЃЌдђ![]() ЃЌЁрДЫЪБ
ЃЌЁрДЫЪБ![]() ЃЌ
ЃЌ![]()
ЁрQ(![]() ЃЌ
ЃЌ![]() )Лђ(
)Лђ(![]() ЃЌ
ЃЌ![]() )ЃЛ
)ЃЛ
ЂкЕБBQ=QCЪБЃЌдђ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрQ(![]() )ЃЛ
)ЃЛ
ЂлЕБBQ=BCЪБЃЌдђ![]() ЃЌНтЕУt=-3,
ЃЌНтЕУt=-3,
ЁрQ(-3ЃЌ1)ЃЛ
злЩЯЫљЪіЃЌШєЁїBQCЮЊЕШбќШ§НЧаЮЃЌдђ
Q(![]() ЃЌ
ЃЌ![]() )Лђ(
)Лђ(![]() ЃЌ
ЃЌ![]() )Лђ(-3ЃЌ1)Лђ(
)Лђ(-3ЃЌ1)Лђ(![]() ).
).


 ПЮГЬДяБъВтЪдОэДГЙи100ЗжЯЕСаД№АИ
ПЮГЬДяБъВтЪдОэДГЙи100ЗжЯЕСаД№АИ аТОэЭѕЦкФЉГхДЬ100ЗжЯЕСаД№АИ
аТОэЭѕЦкФЉГхДЬ100ЗжЯЕСаД№АИ ШЋФмДГЙи100ЗжЯЕСаД№АИ
ШЋФмДГЙи100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЗДБШР§КЏЪ§
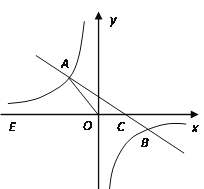
ЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкЖўЁЂЫФЯѓЯоФкЕФAЁЂBСНЕуЃЌгыxжсНЛгкCЕуЃЌЕуAЕФзјБъЮЊЃЈ- 3ЃЌ4ЃЉЃЌЕуBЕФзјБъЮЊ(6ЃЌn).
ЕФЭМЯѓНЛгкЖўЁЂЫФЯѓЯоФкЕФAЁЂBСНЕуЃЌгыxжсНЛгкCЕуЃЌЕуAЕФзјБъЮЊЃЈ- 3ЃЌ4ЃЉЃЌЕуBЕФзјБъЮЊ(6ЃЌn).
ЃЈ1ЃЉЧѓИУЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉСЌНгOBЃЌЧѓЁїAOB ЕФУцЛ§ЃЛ
ЃЈ3ЃЉдкxжсЩЯЪЧЗёДцдкЕуPЃЌЪЙЁїAPCЪЧжБНЧШ§НЧаЮ. ШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГБЈЩчЮЊСЫНтЪаУёЖдЁАЩчЛсжївхКЫаФМлжЕЙлЁБЕФжЊЯўГЬЖШЃЌВЩШЁЫцЛњГщбљЕФЗНЪННјааЮЪОэЕїВщЃЌЕїВщНсЙћЗжЮЊЁАA.ЗЧГЃСЫНтЁБЁЂЁАB.СЫНтЁБЁЂЁАC.ЛљБОСЫНтЁБШ§ИіЕШМЖЃЌВЂИљОнЕїВщНсЙћЛцжЦСЫШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎ
(1)етДЮЕїВщЕФЪаУёШЫЪ§ЮЊ________ШЫЃЌmЃН________ЃЌnЃН________ЃЛ
(2)ВЙШЋЬѕаЮЭГМЦЭМЃЛ
(3)ШєИУЪадМгаЪаУё100000ШЫЃЌЧыФуИљОнГщбљЕїВщЕФНсЙћЃЌЙРМЦИУЪаДѓдМгаЖрЩйШЫЖдЁАЩчЛсжївхКЫаФМлжЕЙлЁБДяЕНЁАA.ЗЧГЃСЫНтЁБЕФГЬЖШЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
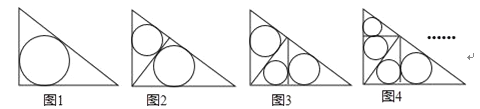
ЁОЬтФПЁПШчЭМ1ЁЋ4ЃЌдкжБНЧБпЗжБ№ЮЊ3КЭ4ЕФжБНЧШ§НЧаЮжаЃЌУПЖрзївЛЬѕаББпЩЯЕФИпОЭдіМгвЛИіШ§НЧаЮЕФФкЧадВЃЌвРДЫРрЭЦЃЌЭМ10жага10ИіжБНЧШ§НЧаЮЕФФкЧадВЃЌЫќУЧЕФУцЛ§ЗжБ№МЧЮЊS1ЃЌS2ЃЌS3ЃЌЁЃЌS10ЃЌдђS1+S2+S3+Ё+S10= ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
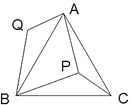
ЁОЬтФПЁПШчЭМЃЌPЪЧЕШБпШ§НЧаЮABCФквЛЕуЃЌНЋЯпЖЮBPШЦЕуBФцЪБеыа§зЊ60ЁуЕУЕНЯпЖЮBQЃЌСЌНгAQЃЎШєPA=4ЃЌPB=5ЃЌPC=3ЃЌдђЫФБпаЮAPBQЕФУцЛ§ЮЊ_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
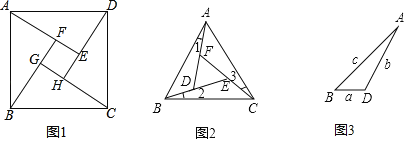
ЁОЬтФПЁПЮЪЬтБГОАЃКШчЭМ1ЃЌдке§ЗНаЮABCDЕФФкВПЃЌзїЁЯDAEЃНЁЯABFЃНЁЯBCGЃНЁЯCDHЃЌИљОнШ§НЧаЮШЋЕШЕФЬѕМўЃЌвзЕУЁїDAEЁеЁїABFЁеЁїBCGЁеЁїCDHЃЌДгЖјЕУЫФБпаЮEFGHЪЧе§ЗНаЮЃЎ
РрБШЬНОПЃКШчЭМ2ЃЌдке§ЁїABCЕФФкВПЃЌзїЁЯ1ЃНЁЯ2ЃНЁЯ3ЃЌADЃЌBEЃЌCFСНСНЯрНЛгкDЃЌEЃЌFШ§ЕуЃЈDЃЌEЃЌFШ§ЕуВЛжиКЯЃЉЃЎ
ЃЈ1ЃЉЁїABDЃЌЁїBCEЃЌЁїCAFЪЧЗёШЋЕШЃПШчЙћЪЧЃЌЧыбЁдёЦфжавЛЖдНјаажЄУїЃЛ
ЃЈ2ЃЉЁїDEFЪЧЗёЮЊе§Ш§НЧаЮЃПЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌНјвЛВНЬНОПЗЂЯжЃЌЁїABDЕФШ§БпДцдквЛЖЈЕФЕШСПЙиЯЕЃЌЩшBDЃНaЃЌADЃНbЃЌABЃНcЃЌЧыЬНЫїaЃЌbЃЌcТњзуЕФЕШСПЙиЯЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
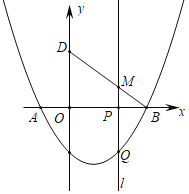
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃН![]() x2+bx+cгыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉгыyжсНЛгкЕуCЃЌЕуDгыЕуCЙигкxжсЖдГЦЃЌЕуPЪЧxжсЩЯЕФвЛИіЖЏЕуЃЌЩшЕуPЕФзјБъЮЊЃЈmЃЌ0ЃЉЃЌЙ§ЕуPзїxжсЕФДЙЯп1ЃЌНЛХзЮяЯпгыЕуQЃЎ
x2+bx+cгыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉгыyжсНЛгкЕуCЃЌЕуDгыЕуCЙигкxжсЖдГЦЃЌЕуPЪЧxжсЩЯЕФвЛИіЖЏЕуЃЌЩшЕуPЕФзјБъЮЊЃЈmЃЌ0ЃЉЃЌЙ§ЕуPзїxжсЕФДЙЯп1ЃЌНЛХзЮяЯпгыЕуQЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБЕуPдкЯпЖЮOBЩЯдЫЖЏЪБЃЌжБЯп1НЛBDгкЕуMЃЌЪдЬНОПmЮЊКЮжЕЪБЃЌЫФБпаЮCQMDЪЧЦНааЫФБпаЮЃЛ
ЃЈ3ЃЉдкЕуPдЫЖЏЕФЙ§ГЬжаЃЌзјБъЦНУцФкЪЧЗёДцдкЕуQЃЌЪЙЁїBDQЪЧвдBDЮЊжБНЧБпЕФжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
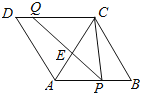
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDЕФБпABЃН8ЃЌЁЯBЃН60ЁуЃЌPЪЧABЩЯвЛЕуЃЌBPЃН3ЃЌQЪЧCDБпЩЯвЛЖЏЕуЃЌНЋЬнаЮAPQDбижБЯпPQелЕўЃЌAЕФЖдгІЕуЮЊAЁфЃЌЕБCAЁфЕФГЄЖШзюаЁЪБЃЌCQЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
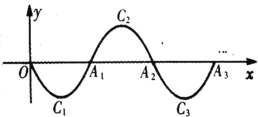
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓМЧЮЊ
ЕФЭМЯѓМЧЮЊ![]() ЃЌЫќгы
ЃЌЫќгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЛНЋ
ЃЛНЋ![]() ШЦЕу
ШЦЕу![]() а§зЊ180ЁуЕУ
а§зЊ180ЁуЕУ![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЛНЋ
ЃЛНЋ![]() ШЦЕу
ШЦЕу![]() а§зЊ180ЁуЕУ
а§зЊ180ЁуЕУ![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЛЁЁШчДЫНјааЯТШЅЃЌЕУЕНвЛЬѕЁАВЈРЫЯпЁБ.Шє
ЃЛЁЁШчДЫНјааЯТШЅЃЌЕУЕНвЛЬѕЁАВЈРЫЯпЁБ.Шє![]() дкетЬѕЁАВЈРЫЯпЁБЩЯЃЌдђ
дкетЬѕЁАВЈРЫЯпЁБЩЯЃЌдђ![]() ____.
____.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com