
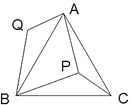
【题目】如图,P是等边三角形ABC内一点,将线段BP绕点B逆时针旋转60°得到线段BQ,连接AQ.若PA=4,PB=5,PC=3,则四边形APBQ的面积为_______.
【答案】![]()
【解析】
由旋转的性质可得△BPQ是等边三角形,由全等三角形的判定可得△ABQ≌△CBP(SAS),由勾股定理的逆定理可得△APQ是直角三角形,求四边形的面积转化为求两个特殊三角形的面积即可.
解:连接PQ,
由旋转的性质可得,BP=BQ,
又∵∠PBQ=60°,
∴△BPQ是等边三角形,
∴PQ=BP,
在等边三角形ABC中,∠CBA=60°,AB=BC,
∴∠ABQ=60°-∠ABP
∠CBP=60°-∠ABP
∴∠ABQ=∠CBP
在△ABQ与△CBP中
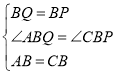 ,
,
∴△ABQ≌△CBP(SAS),
∴AQ=PC,
又∵PA=4,PB=5,PC=3,
∴PQ=BP=5,PC=AQ=3,
在△APQ中,因为![]() ,25=16+9,
,25=16+9,
∴由勾股定理的逆定理可知△APQ是直角三角形,
∴![]() ,
,
故答案为:![]()



科目:初中数学 来源: 题型:
【题目】张老师在讲解复习《圆》的内容时,用投影仪屏幕展示出如下内容:
如图,![]() 内接于
内接于![]() ,直径
,直径![]() 的长为2,过点
的长为2,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
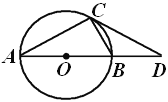
张老师让同学们添加条件后,编制一道题目,并按要求完成下列填空.
(1)在屏幕内容中添加条件![]() ,则
,则![]() 的长为______.
的长为______.
(2)以下是小明、小聪的对话:
小明:我加的条件是![]() ,就可以求出
,就可以求出![]() 的长
的长
小聪:你这样太简单了,我加的是![]() ,连结
,连结![]() ,就可以证明
,就可以证明![]() 与
与![]() 全等.
全等.
参考上面对话,在屏幕内容中添加条件,编制一道题目(此题目不解答,可以添线、添字母).______.
查看答案和解析>>
科目:初中数学 来源: 题型:
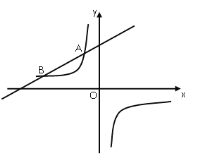
【题目】如图,一次函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像与反比例函数
)的图像与反比例函数![]() 的图像交于
的图像交于![]() ,
,![]() 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线![]() 向下平移
向下平移![]() 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
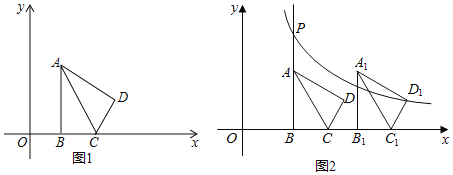
【题目】如图1,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限,B,C在x轴的正半轴上(C在B的右侧),BC=2,AB=2![]() ,△ADC与△ABC关于AC所在的直线对称.
,△ADC与△ABC关于AC所在的直线对称.
(1)当OB=2时,求点D的坐标;
(2)若点A和点D在同一个反比例函数的图象上,求OB的长;
(3)如图2,将第(2)题中的四边形ABCD向右平移,记平移后的四边形为A1B1C1D1,过点D1的反比例函数y=![]() (k≠0)的图象与BA的延长线交于点P.问:在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.
(k≠0)的图象与BA的延长线交于点P.问:在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是小明在健身器材上进行仰卧起坐锻炼时的情景,图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图.已知AC=0.66米,BD=0.26米,α=20°.(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)

(1)求AB的长(精确到0.01米);
(2)若测得ON=0.8米,试计算小明头顶由N点运动到M点的路径![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
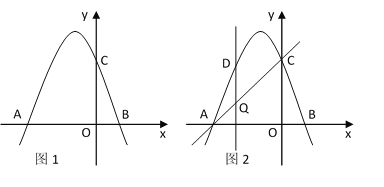
【题目】如图1,抛物线y=﹣x2+bx+c交x轴于点A(- 4,0)和点B,交y轴于点C(0,4).
(1)求抛物线的函数表达式;
(2)如图2,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,当△ADC面积有最大值时,在抛物线对称轴上找一点M,使DM+AM的值最小,求出此时M的坐标;
(3)点Q在直线AC上的运动过程中,是否存在点Q,使△BQC为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
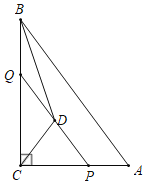
【题目】如图,在Rt△ABC中,∠C=90°,点P是边AC上一点,过点P作PQ∥AB交BC于点Q,D为线段PQ的中点,BD平分∠ABC,以下四个结论①△BQD是等腰三角形;②BQ=DP;③PA=![]() QP;④
QP;④![]() =(1+
=(1+![]() )2;其中正确的结论的个数( )
)2;其中正确的结论的个数( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克,规定销售单价不低于成本,又不高于成本的两倍.经过市场调查发现,某天西瓜的销售量y(千克)与销售单价x(元/千克)的函数关系如下图所示:
(1)求y与x的函数解析式(也称关系式);
(2)求这一天销售西瓜获得的利润的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
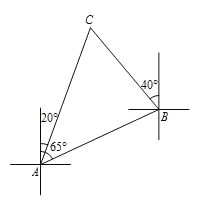
【题目】如图,一艘船由A港沿北偏东65°方向航行![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
求:(1)∠C的度数;
(2)A,C两港之间的距离为多少km.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com