
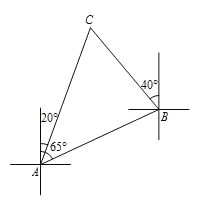
【题目】如图,一艘船由A港沿北偏东65°方向航行![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
求:(1)∠C的度数;
(2)A,C两港之间的距离为多少km.
【答案】(1)∠C=60°(2)AC=![]()
【解析】
(1)根据方位角的概念确定∠ACB=40°+20°=60;
(2)AB=30![]() ,过B作BE⊥AC于E,解直角三角形即可得到结论.
,过B作BE⊥AC于E,解直角三角形即可得到结论.
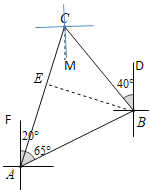
解:(1)如图,在点C处建立方向标
根据题意得,AF∥CM∥BD
∴∠ACM=∠FAC, ∠BCM=∠DBC
∴∠ACB=∠ACM+∠BCM=40°+20°=60°,
(2)∵AB=30![]() ,过B作BE⊥AC于E,
,过B作BE⊥AC于E,
∴∠AEB=∠CEB=90°,
在Rt△ABE中,∵∠ABE=45°,AB=30![]() ,
,
∴AE=BE=![]() AB=30km,
AB=30km,
在Rt△CBE中,∵∠ACB=60°,
∴CE=![]() BE=10
BE=10![]() km,
km,
∴AC=AE+CE=30+10![]() ,
,
∴A,C两港之间的距离为(30+10![]() )km,
)km,


科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司种植和销售一种野山菌,已知该野山菌的成本是12元/千克,规定销售价格不低于成本,又不高于成本的两倍.经过市场调查发现,某天该野山菌的销售量y(千克)与销售价格x(元/千克)的函数关系如图所示:
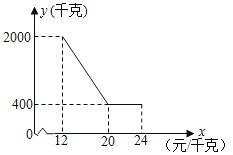
(1)求y与x之间的函数关系式;
(2)求这一天销售野山菌获得的利润W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
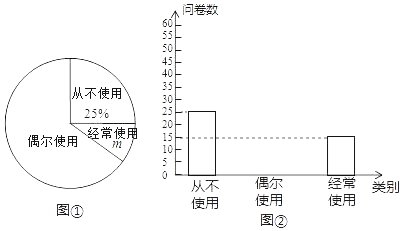
【题目】“低碳生活,绿色出行”是我们倡导的一种生活方式,某校为了解学生对共享单车的使用情况,随机抽取部分学生进行问卷调查,并将这次调查的结果绘制了以下两幅不完整的统计图.
根据所给信息,解答下列问题:
(1)m= ;
(2)补全条形统计图;
(3)这次调查结果的众数是 ;
(4)已知全校共3000名学生,请估计“经常使用”共享单车的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12米,BC=24米,动点P从点A开始沿边AB向B以2米/秒的速度运动(不与点B重合),动点Q从点B开始沿BC向C以4米/秒的速度运动(不与点C重合).如果P、Q分别从A、B同时出发,设运动时间为x秒,四边形APQC的面积为y平方米.
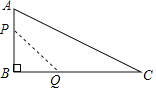
(1)求y与x之间的函数关系式,直接写出自变量x的取值范围;
(2)求当x为多少时,y有最小值,最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴分别交于A(﹣3,0),B两点,与y轴交于点C,抛物线的顶点E(﹣1,4),对称轴交x轴于点F.
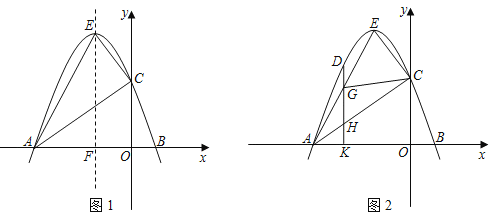
(1)请直接写出这条抛物线和直线AE、直线AC的解析式;
(2)连接AC、AE、CE,判断△ACE的形状,并说明理由;
(3)如图2,点D是抛物线上一动点,它的横坐标为m,且﹣3<m<﹣1,过点D作DK⊥x轴于点K,DK分别交线段AE、AC于点G、H.在点D的运动过程中,
①DG、GH、HK这三条线段能否相等?若相等,请求出点D的坐标;若不相等,请说明理由;
②在①的条件下,判断CG与AE的数量关系,并直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区商店销售一种纪念品,每件的进货价为40元.经市场调研,当该纪念品每件的销售价为50元时,每天可销售200件;当每件的销售价每增加1元,每天的销售数量将减少10件.
(1)当销售该纪念品每天能获得利润2160元时,每件的销售价应为多少?
(2)当每件的销售价为多少时,销售该纪念品每天获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC=4,BC=6点D在底边BC上,且∠DAC=∠ACD,将△ACD沿着AD所在直线翻折,使得点C落到点E处,联结BE,那么BE的长为______.
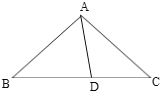
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.

(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com