
【题目】如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.
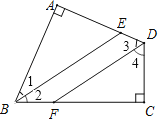
【答案】BE∥DF.理由见解析
【解析】
试题分析:根据四边形的内角和定理和∠A=∠C=90°,得∠ABC+∠ADC=180°;根据角平分线定义、等角的余角相等易证明和BE与DF两条直线有关的一对同位角相等,从而证明两条直线平行.
解:BE∥DF.理由如下:
∵∠A=∠C=90°(已知),
∴∠ABC+∠ADC=180°(四边形的内角和等于360°).
∵BE平分∠ABC,DF平分∠ADC,
∴∠1=∠2=![]() ∠ABC,∠3=∠4=
∠ABC,∠3=∠4=![]() ∠ADC(角平分线的定义).
∠ADC(角平分线的定义).
∴∠1+∠3=![]() (∠ABC+∠ADC)=
(∠ABC+∠ADC)=![]() ×180°=90°(等式的性质).
×180°=90°(等式的性质).
又∠1+∠AEB=90°(三角形的内角和等于180°),
∴∠3=∠AEB(同角的余角相等).
∴BE∥DF(同位角相等,两直线平行).


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】随着居民经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭,抽样调查显示,截止2015年底某市汽车拥有量为16.9万辆.己知2013年底该市汽车拥有量为10万辆,设2013年底至2015年底该市汽车拥有量的平均增长率为x,根据题意列方程得( )
A.10(1+x)2=16.9 B.10(1+2x)=16.9
C.10(1﹣x)2=16.9 D.10(1﹣2x)=16.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE。
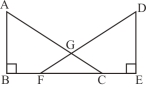
求证:(1)△ABC≌△DEF;
(2)GF=GC。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距40千米,中午12:00时,甲从A地出发开车到B地,12:10时乙从B地出发骑自行车到A地,设甲行驶的时间为t(分),甲、乙两人离A地的距离S(千米)与时间t(分)之间的关系如图所示.由图中的信息可知,乙到达A地的时间为( )
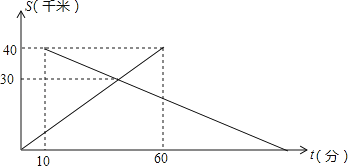
A.14:00 B.14:20 C.14:30 D.14:40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
![]()
(1)写出数轴上A、B两点表示的数;
(2)动点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒1个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,t为何值时,原点O、与P、Q三点中,有一点恰好是另两点所连线段的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
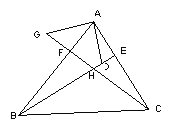
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。
求证:(1)AD=AG,(2)AD与AG的位置关系如何。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com