
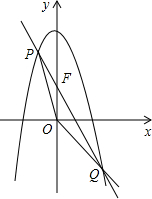
 抛物线y=-x2+10,直线l过点F(0,4),交抛物线于P、Q两点,是否存在直线l,使S△POF:S△QOF=1:3?若存在,求直线l的解析式;若不存在,请说明理由.
抛物线y=-x2+10,直线l过点F(0,4),交抛物线于P、Q两点,是否存在直线l,使S△POF:S△QOF=1:3?若存在,求直线l的解析式;若不存在,请说明理由. 分析 根据直线l过F(0,4),设直线l的解析式为y=kx+4,根据题意设P(a,-a2+10),Q(-3a,-9a2+10),代入直线l的解析式y=kx+4,即可求得k的值,进而求得直线l的解析式.
解答 解:设P(a,-a2+10),
∵S△EOC:S△FOC=1:3,
∴Q(-3a,-9a2+10),
∵直线与y轴的交点坐标为(0,4),
∴设直线l的解析式为y=kx+4,
把P、Q代入得
$\left\{\begin{array}{l}{-{a}^{2}+10=ak+4}\\{-9{a}^{2}+10=-3ak+4}\end{array}\right.$,
解得k=±2$\sqrt{2}$,
∴直线l的解析式为y=2$\sqrt{2}$x+4或y=-2$\sqrt{2}$x+4.
点评 本题考查了二次函数的性质,待定系数法求一次函数的解析式,分析出P、Q两点的横坐标的特点是解题的关键.


科目:初中数学 来源: 题型:解答题
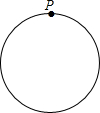 有一长为240米的圆形跑道,小明和他的小狗同时从跑道的点P处出发沿顺时针方向跑步,已知小明的速度为4米/秒,小狗的速度为12米/秒,跑步的时间记为t秒,在跑步过程中,小明和他的小狗之间相距(取两者之间较短一段圆弧跑道的长度)为w米
有一长为240米的圆形跑道,小明和他的小狗同时从跑道的点P处出发沿顺时针方向跑步,已知小明的速度为4米/秒,小狗的速度为12米/秒,跑步的时间记为t秒,在跑步过程中,小明和他的小狗之间相距(取两者之间较短一段圆弧跑道的长度)为w米查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com