
 有一长为240米的圆形跑道,小明和他的小狗同时从跑道的点P处出发沿顺时针方向跑步,已知小明的速度为4米/秒,小狗的速度为12米/秒,跑步的时间记为t秒,在跑步过程中,小明和他的小狗之间相距(取两者之间较短一段圆弧跑道的长度)为w米
有一长为240米的圆形跑道,小明和他的小狗同时从跑道的点P处出发沿顺时针方向跑步,已知小明的速度为4米/秒,小狗的速度为12米/秒,跑步的时间记为t秒,在跑步过程中,小明和他的小狗之间相距(取两者之间较短一段圆弧跑道的长度)为w米分析 (1)小狗与小明相遇的时间为240÷(12-4)=30秒,也就是说当t≤15时,w=(12-4)t;当15≤t≤30时,w=240-(12-4)t,由此代入求得答案即可.
(2)分段表示即可;
(3)利用(2)直接得出答案即可.
解答 解:(1)当t=15秒,W=15×(12-4)=120米,
当t=30秒时,240-30×(12-4)=0米;
(2)当0<t≤15时,w=(12-4)t=8t;
当15<t≤30时,w=240-(12-4)t=240-8t;
当30<t≤45时,w=(12-4)(t-30)=8t-240;
当45<t≤60时,w=240-(12-4)(t-45)=600-8t;
(3)当600<t≤615时,w=(12-4)(t-600)=8t-4800;
当615<t≤630时,w=240-(12-4)(t-600)=5040-8t.
点评 此题考查列代数式,分时间段考虑是解决问题的关键.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
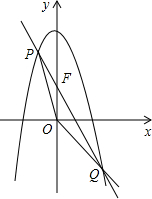 抛物线y=-x2+10,直线l过点F(0,4),交抛物线于P、Q两点,是否存在直线l,使S△POF:S△QOF=1:3?若存在,求直线l的解析式;若不存在,请说明理由.
抛物线y=-x2+10,直线l过点F(0,4),交抛物线于P、Q两点,是否存在直线l,使S△POF:S△QOF=1:3?若存在,求直线l的解析式;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com