
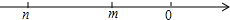
分析 首先根据数m,n在数轴上的位置,可得n<m<0,据此判断出-m、m-n、m+n的正负;然后根据整式的加减运算方法,求出算式-(m+n)-|-m|+|m-n|-2|m+n|的值是多少即可.
解答 解:根据图示,可得
n<m<0,
∴-m>0,m-n>0,m+n<0,
∴-(m+n)-|-m|+|m-n|-2|m+n|
=-m-n-(-m)+m-n+2(m+n)
=-m-n+m+m-n+2m+2n
=3m
点评 (1)此题主要考查了整式的加减运算,要熟练掌握,解答此题的关键是要明确:整式的加减的实质就是去括号、合并同类项.一般步骤是:先去括号,然后合并同类项.
(2)此题还考查了数轴的特征和应用,要熟练掌握,解答此题的关键是要明确:一般来说,当数轴方向朝右时,右边的数总比左边的数大.
(3)此题还考查了绝对值的含义和应用,要熟练掌握,解答此题的关键是要明确:①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数-a;③当a是零时,a的绝对值是零.


科目:初中数学 来源: 题型:解答题
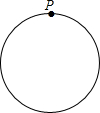 有一长为240米的圆形跑道,小明和他的小狗同时从跑道的点P处出发沿顺时针方向跑步,已知小明的速度为4米/秒,小狗的速度为12米/秒,跑步的时间记为t秒,在跑步过程中,小明和他的小狗之间相距(取两者之间较短一段圆弧跑道的长度)为w米
有一长为240米的圆形跑道,小明和他的小狗同时从跑道的点P处出发沿顺时针方向跑步,已知小明的速度为4米/秒,小狗的速度为12米/秒,跑步的时间记为t秒,在跑步过程中,小明和他的小狗之间相距(取两者之间较短一段圆弧跑道的长度)为w米查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知数轴上两点A,B对应的数分别为-1,3,P为数轴上的动点,其对应的数为x.
已知数轴上两点A,B对应的数分别为-1,3,P为数轴上的动点,其对应的数为x.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com