
分析 (1)根据例题方程两边同时除以x,即可求得x+$\frac{1}{x}$的值,然后平方即可求得x2+$\frac{1}{{x}^{2}}$的值,然后再平方求得x4+$\frac{1}{{x}^{4}}$的值;
(2)首先方程两边除以2x即可求得x+$\frac{1}{x}$的值,然后平方即可求得x2+$\frac{1}{{x}^{2}}$的值,然后利用立方差公式求解.
解答 解:(1)方程两边同时乘以$\frac{1}{x}$得:x-4+$\frac{1}{x}$=0,则x+$\frac{1}{x}$=4,
两边平方得x2+$\frac{1}{{x}^{2}}$+2=16,则x2+$\frac{1}{{x}^{2}}$=14,
两边平方得x4+$\frac{1}{{x}^{4}}$+2=196,则x4+$\frac{1}{{x}^{4}}$=194.
故答案是:14,194;
(2)方程两边同时除以2x得x-$\frac{7}{2}$+$\frac{1}{x}$=0,
则x+$\frac{1}{x}$=$\frac{7}{2}$,
两边平方得x2+$\frac{1}{{x}^{2}}$+2=$\frac{49}{4}$,则x2+$\frac{1}{{x}^{2}}$=$\frac{41}{4}$,
x3+$\frac{1}{{x}^{3}}$=(x+$\frac{1}{x}$)(x2+$\frac{1}{{x}^{2}}$-1)=$\frac{7}{2}$×($\frac{41}{4}$-1)=$\frac{7}{2}$×$\frac{37}{4}$=$\frac{259}{8}$.
点评 本题考查平方差公式以及立方差公式,正确理解平方差公式的变形是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
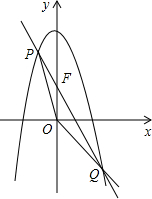 抛物线y=-x2+10,直线l过点F(0,4),交抛物线于P、Q两点,是否存在直线l,使S△POF:S△QOF=1:3?若存在,求直线l的解析式;若不存在,请说明理由.
抛物线y=-x2+10,直线l过点F(0,4),交抛物线于P、Q两点,是否存在直线l,使S△POF:S△QOF=1:3?若存在,求直线l的解析式;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
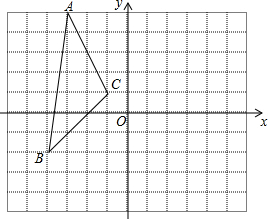 如图,直角坐标系中,A(-3,5),B(-4,-2),C(-1,1).
如图,直角坐标系中,A(-3,5),B(-4,-2),C(-1,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com