
分析 (1)把等号左边的数都能整理成以2为底数的幂相乘,再根据同底数幂相乘,底数不变指数相加计算,然后根据指数相等列式求解即可;
(2)先根据幂的乘方的法则分别求出32m和34n的值,然后根据同底数幂的除法法则求解
解答 解:(1)2•8n•16n,
=2×23n×24n,
=27n+1,
∵2•8n•16n=222,
∴7n+1=22,
解得n=3;
(2)∵3m=6,9n=2,
∴32m=(3m)2=36,34n=(32n)2=(9n)2=4,
则32m-4n=$\frac{{3}^{2m}}{{3}^{4n}}$=$\frac{36}{4}$=9.
点评 本题主要考查同底数幂的乘法的性质,熟练掌握性质是解题的关键.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:解答题
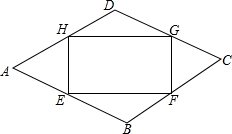 如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,已知∠A=60°.
如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,已知∠A=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
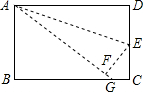 如图,点E是矩形ABCD的边CD的中点,将△ADE沿AE折叠后得到△AEF,点F在矩形ABCD内部,延长AF交BC于G.
如图,点E是矩形ABCD的边CD的中点,将△ADE沿AE折叠后得到△AEF,点F在矩形ABCD内部,延长AF交BC于G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-4x=3 | B. | $\frac{y}{2}$+2y=3 | C. | x+2y=1 | D. | x-1=$\frac{1}{x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com